题目内容
设两向量
,
满足|
|=2,|
|=1,
、
的夹角为60°,
(1)试求|3
+
|
(2)若向量2t
+7
与向量
+t
的夹角余弦值为非负值,求实数t的取值范围.
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
(1)试求|3
| e1 |
| e2 |
(2)若向量2t
| e1 |
| e2 |
| e1 |
| e2 |
分析:(1)利用向量的数量积公式,结合题意算出
•
=1.再由向量模的公式和数量积的运算性质加以计算,即可算出|3
+
|的值;
(2)根据题意,可得2t
+7
与
+t
的数量积大于或等于0,由此建立关于
2、
•
、
2和t的不等式,代入数据化简得到关于t的一元二次不等式,解之即可得出实数t的取值范围.
| e1 |
| e2 |
| e1 |
| e2 |
(2)根据题意,可得2t
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e1 |
| e2 |
| e2 |
解答:解:(1)由题意,可得
∵|
|=2,|
|=1,
、
的夹角为60°,
∴
•
=|
|•|
|cos60°=1.
因此,|3
+
|=
=
=
=
;
(2)∵向量2t
+7
与向量
+t
的夹角余弦值为非负值,
∴(2t
+7
)•(
+t
)≥0,
即2t
2+(7+2t2)
•
+7t
2≥0,
∵|
|=2,|
|=1,
•
=1,
∴不等式可化为2t×4+(7+2t2)×1+7t×1≥0,
化简得2t2+15t+7≥0,
解得t≤-7或t≥-
.
即满足条件的实数t的取值范围为:(-∞,-7]∪[-
,+∞).
∵|
| e1 |
| e2 |
| e1 |
| e2 |
∴
| e1 |
| e2 |
| e1 |
| e2 |
因此,|3
| e1 |
| e2 |
(3
|
9|
|
=
| 9×22+6×1+12 |
| 43 |
(2)∵向量2t
| e1 |
| e2 |
| e1 |
| e2 |
∴(2t
| e1 |
| e2 |
| e1 |
| e2 |
即2t
| e1 |
| e1 |
| e2 |
| e2 |
∵|
| e1 |
| e2 |
| e1 |
| e2 |
∴不等式可化为2t×4+(7+2t2)×1+7t×1≥0,
化简得2t2+15t+7≥0,
解得t≤-7或t≥-
| 1 |
| 2 |
即满足条件的实数t的取值范围为:(-∞,-7]∪[-
| 1 |
| 2 |
点评:本题给出向量
、
的模与夹角,求3
+
的模,并讨论2t
+7
与
+t
的夹角问题.着重考查了平面向量的数量积及其运算性质、向量模的公式和一元二次不等式的解法等知识,属于中档题.
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |

练习册系列答案
相关题目
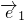 |=2,|
|=2,|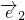 |=1,
|=1,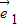 |=2,|
|=2,| |=1,
|=1,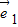 、
、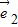 的夹角为60°,若向量2t
的夹角为60°,若向量2t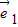 +7
+7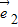 与向量
与向量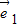 +t
+t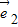 的夹角为钝角,求实数t的取值范围.
的夹角为钝角,求实数t的取值范围.