题目内容
设两向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为钝角,求实数t的取值范围.解:∵![]() =4,
=4,![]() =1,e1·e2=2×1×cos60°,
=1,e1·e2=2×1×cos60°,
∴(2te1+7e2)·(e1+te2)=2t![]() +(2t2+7)
+(2t2+7)
e1·e2+7t![]() =2t2+15t+7.∴2t2+15t+7<0.
=2t2+15t+7.∴2t2+15t+7<0.
∴-7<t<![]() .
.
设2te1+7e2=λ(e1+te2)(λ<0),
则2t=λ,且7=tλ,
∴2t2=7.
∴t=![]() ,λ=
,λ=![]() .∴t=
.∴t=![]() 时,
时,
2te1+7e2与e1+te2的夹角为π,故t的取值范围是(-7,![]() )∪(
)∪(![]() ,
,![]() ).
).

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
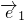 |=2,|
|=2,|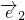 |=1,
|=1,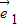 |=2,|
|=2,| |=1,
|=1,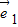 、
、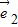 的夹角为60°,若向量2t
的夹角为60°,若向量2t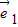 +7
+7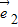 与向量
与向量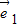 +t
+t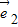 的夹角为钝角,求实数t的取值范围.
的夹角为钝角,求实数t的取值范围.