题目内容
设两向量e1、e2满足|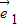 |=2,|
|=2,| |=1,
|=1,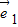 、
、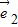 的夹角为60°,若向量2t
的夹角为60°,若向量2t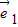 +7
+7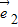 与向量
与向量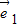 +t
+t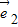 的夹角为钝角,求实数t的取值范围.
的夹角为钝角,求实数t的取值范围.
【答案】分析:欲求实数t的取值范围,先根据条件,利用向量积的运算求出(2t +7
+7 )•(
)•( +t
+t )的值,由于夹角为钝角,所以计算得到的值是负值,最后解出这个不等式即可得到实数t的取值范围.
)的值,由于夹角为钝角,所以计算得到的值是负值,最后解出这个不等式即可得到实数t的取值范围.
解答:解: 2=4,
2=4, 2=1,
2=1, •
• =2×1×cos60°=1,
=2×1×cos60°=1,
∴(2t +7
+7 )•(
)•( +t
+t )=2t
)=2t 2+(2t2+7)
2+(2t2+7) •
• +7t
+7t 2=2t2+15t+7.
2=2t2+15t+7.
∴2t2+15t+7<0.
∴-7<t<- .设2t
.设2t +7
+7 =λ(
=λ( +t
+t )(λ<0)⇒
)(λ<0)⇒ ⇒2t2=7⇒t=-
⇒2t2=7⇒t=- ,
,
∴λ=- .
.
∴当t=- 时,2t
时,2t +7
+7 与
与 +t
+t 的夹角为π.
的夹角为π.
∴t的取值范围是(-7,- )∪(-
)∪(- ,-
,- ).
).
点评:本题考查平面向量积的运算,同时考查一元二次不等式的解法.
 +7
+7 )•(
)•( +t
+t )的值,由于夹角为钝角,所以计算得到的值是负值,最后解出这个不等式即可得到实数t的取值范围.
)的值,由于夹角为钝角,所以计算得到的值是负值,最后解出这个不等式即可得到实数t的取值范围.解答:解:
 2=4,
2=4, 2=1,
2=1, •
• =2×1×cos60°=1,
=2×1×cos60°=1,∴(2t
 +7
+7 )•(
)•( +t
+t )=2t
)=2t 2+(2t2+7)
2+(2t2+7) •
• +7t
+7t 2=2t2+15t+7.
2=2t2+15t+7.∴2t2+15t+7<0.
∴-7<t<-
 .设2t
.设2t +7
+7 =λ(
=λ( +t
+t )(λ<0)⇒
)(λ<0)⇒ ⇒2t2=7⇒t=-
⇒2t2=7⇒t=- ,
,∴λ=-
 .
.∴当t=-
 时,2t
时,2t +7
+7 与
与 +t
+t 的夹角为π.
的夹角为π.∴t的取值范围是(-7,-
 )∪(-
)∪(- ,-
,- ).
).点评:本题考查平面向量积的运算,同时考查一元二次不等式的解法.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
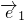 |=2,|
|=2,|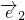 |=1,
|=1,