题目内容
定义在R上的单调函数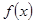 满足
满足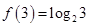 且对任意
且对任意 都有
都有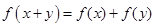 .
.
(1)求证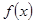 为奇函数;
为奇函数;
(2)若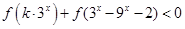 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)证明:利用“赋值法”,确定f(0)=0,再
计算f(x)+f(-x)=0.
(2) t=3 >0,换元后,问题等价于t
>0,换元后,问题等价于t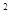 -(1+k)t+2>0
-(1+k)t+2>0
假设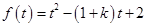 ,当
,当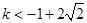 时,
时,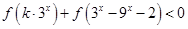 对任意
对任意 恒成立.
恒成立.
解析试题分析:
思路分析:(1)证明:利用“赋值法”,确定f(0)=0,再
计算f(x)+f(-x)=0.
(2) t=3 >0,换元后,问题等价于t
>0,换元后,问题等价于t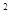 -(1+k)t+2>0
-(1+k)t+2>0
假设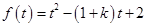 ,应用二次函数的图象和性质进一步求解。
,应用二次函数的图象和性质进一步求解。
(1)证明:f(x+y)=f(x)+f(y) (x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,
则有0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,
所以f(x)是奇函数.
(2)解: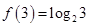 >0,即f(3)>f(0),又
>0,即f(3)>f(0),又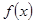 在R上是单调函数,
在R上是单调函数,
所以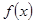 在R上是增函数
在R上是增函数
又由(1)f(x)是奇函数.f(k·3 )<-f(3
)<-f(3 -9
-9 -2)=f(-3
-2)=f(-3 +9
+9 +2),
+2),
∴ k·3 <-3
<-3 +9
+9 +2,3
+2,3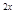 -(1+k)·3
-(1+k)·3 +2>0对任意x∈R成立.
+2>0对任意x∈R成立.
令t=3 >0,问题等价于t
>0,问题等价于t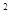 -(1+k)t+2>0
-(1+k)t+2>0
对任意t>0恒成立.
令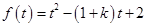 ,其对称轴
,其对称轴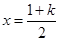
当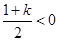 即
即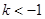 时,
时,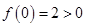 符合题意;
符合题意;
当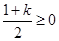 时,对任意
时,对任意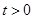 ,
,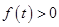 恒成立
恒成立
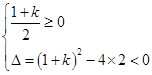
解得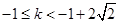
综上所述,当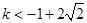 时,
时,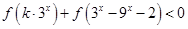 对任意
对任意 恒成立.
恒成立.
考点:函数的单调性,指数函数的性质,二次函数的图象和性质。
点评:中档题,本题涉及抽象函数问题,一般要考虑应用“赋值法”,确定所需数据。本题通过换元,将问题转化成二次函数的图象和性质应用问题,具有“化生为熟”的示范作用。

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案已知函数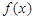 的定义域为
的定义域为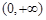 ,若
,若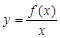 在
在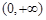 上为增函数,则称
上为增函数,则称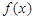 为“一阶比增函数”;若
为“一阶比增函数”;若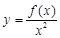 在
在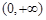 上为增函数,则称
上为增函数,则称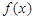 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为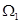 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为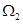 .
.
(Ⅰ)已知函数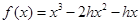 ,若
,若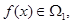 且
且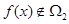 ,求实数
,求实数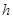 的取值范围;
的取值范围;
(Ⅱ)已知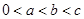 ,
,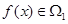 且
且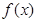 的部分函数值由下表给出,
的部分函数值由下表给出,
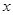 |  | 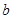 | 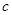 |  |
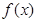 | 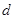 | 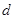 | 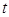 | 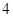 |
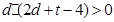 ;
;(Ⅲ)定义集合

请问:是否存在常数
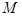 ,使得
,使得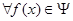 ,
,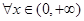 ,有
,有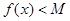 成立?若存在,求出
成立?若存在,求出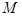 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由. 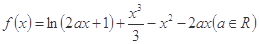
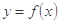 在
在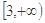 上为增函数,求实数
上为增函数,求实数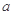 的取值范围;
的取值范围;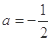 时,方程
时,方程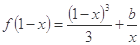 有实根,求实数
有实根,求实数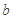 的最大值.
的最大值.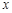 的空气隔层.根据热传导知识,对于厚度为
的空气隔层.根据热传导知识,对于厚度为 的均匀介质,两侧的温度差为
的均匀介质,两侧的温度差为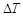 ,单位时间内,在单位面积上通过的热量
,单位时间内,在单位面积上通过的热量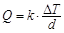 ,其中
,其中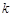 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为
为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为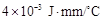 ,空气的热传导系数为
,空气的热传导系数为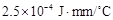 .)
.)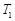 ,
,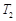 ,内层玻璃外侧温度为
,内层玻璃外侧温度为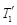 ,外层玻璃内侧温度为
,外层玻璃内侧温度为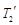 ,且
,且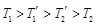 .试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用
.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用
 ,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.
,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.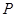 :函数
:函数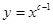 在
在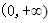 上为减函数, 命题
上为减函数, 命题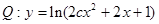 的值域为
的值域为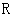 ,命题
,命题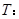 函数
函数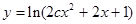 定义域为
定义域为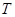 为真命题,求
为真命题,求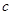 的取值范围。
的取值范围。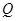 为真命题,
为真命题,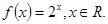
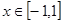 ,使得
,使得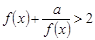 成立,求实数
成立,求实数 的取值范围;
的取值范围;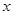 的不等式
的不等式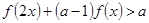 ;
; ,求
,求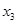 的最大值.
的最大值. 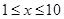 ),每小时可获得利润是
),每小时可获得利润是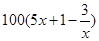 元.
元.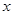 满足不等式
满足不等式 ,求函数
,求函数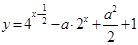 的最小值.
的最小值.