题目内容
如图,若F1、F2为双曲线![]() 的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且四边形OMPF1为菱形.
的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且四边形OMPF1为菱形.

(Ⅰ)若此双曲线过点![]() ,求双曲线的方程;
,求双曲线的方程;
(Ⅱ)设(Ⅰ)中双曲线的虚轴端点为B1、B2(B1在y轴的正半轴上),过B2作直线l与双曲线交于A、B两点,当![]() 时,求直线l的方程.
时,求直线l的方程.
答案:
解析:
解析:
|
解(Ⅰ)∵四边形PF1OM是菱形,设半焦距为c,则有|OF1|=|PF1|=|PM|=c, ∴|PF2|=|PF1|=2a=c=2a.由双曲线第二定义得 即 又 设双曲线方程为 ∵双曲线过点N(2, ∴所求双曲线的方程为 (Ⅱ)由题意知B1(0,3)、B2(0,-3),设直线l的方程为 则由 ∵双曲线的渐近线为 即 ∵ ∴ 又∵ 而 ∴ 即 ∴直线l的方程为 |

练习册系列答案
相关题目
 消去y得
消去y得 (文)如图所示:已知椭圆C:
(文)如图所示:已知椭圆C:
 =
=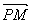 .
.
 =
= .
.