题目内容
在△OAB中,
(1)若C为直线AB上一点,且 ,求证:
,求证: ;
;
(2)若 ,
, ,且C为线段AB上靠近A的一个三等分点,求
,且C为线段AB上靠近A的一个三等分点,求 的值;
的值;
(3)若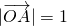 ,
, ,且P1,P2,P3,…,Pn-1为线段AB的n(n≥2)个等分点,求
,且P1,P2,P3,…,Pn-1为线段AB的n(n≥2)个等分点,求 的值.
的值.
解:(1)由 ,得
,得 .
.
即 ,因为λ≠-1,所以
,因为λ≠-1,所以 .(4分)
.(4分)
(2) (6分)
(6分)
因为 ,
, ,所以
,所以 .
.
由于C为线段AB上靠近A的一个三等分点,故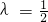
所以 (8分)
(8分)
(3) =
=
= (10分)
(10分)
=
= =
= =n-1(14分)
=n-1(14分)
分析:(1)由 ,得
,得 .然后求出
.然后求出 即可证明结论.
即可证明结论.
(2)利用(1)化简 ,结合
,结合 ,
, ,求出λ,推出
,求出λ,推出 的值.
的值.
(3)利用(1)的结论,化简 为
为 ,求出它的值.
,求出它的值.
点评:本题考查平面向量数量积的运算,考查计算能力,是中档题.
 ,得
,得 .
.即
 ,因为λ≠-1,所以
,因为λ≠-1,所以 .(4分)
.(4分)(2)
 (6分)
(6分)因为
 ,
, ,所以
,所以 .
.由于C为线段AB上靠近A的一个三等分点,故
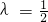
所以
 (8分)
(8分)(3)
 =
=
=
 (10分)
(10分)=

=
 =
= =n-1(14分)
=n-1(14分)分析:(1)由
 ,得
,得 .然后求出
.然后求出 即可证明结论.
即可证明结论.(2)利用(1)化简
 ,结合
,结合 ,
, ,求出λ,推出
,求出λ,推出 的值.
的值.(3)利用(1)的结论,化简
 为
为 ,求出它的值.
,求出它的值.点评:本题考查平面向量数量积的运算,考查计算能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
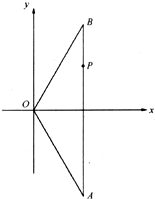 (2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.
(2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2. ,求证:
,求证: ;
; ,
, ,且C为线段AB上靠近A的一个三等分点,求
,且C为线段AB上靠近A的一个三等分点,求 的值;
的值; ,
, ,且P1,P2,P3,…,Pn-1为线段AB的n(n≥2)个等分点,求
,且P1,P2,P3,…,Pn-1为线段AB的n(n≥2)个等分点,求 的值.
的值.