题目内容
【题目】在![]() 中,设边
中,设边![]() ,
,![]() ,
,![]() 所对的角分别为
所对的角分别为![]() ,
,![]() ,
,![]() ,已知
,已知![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用正弦定理可将原式化简为cosA![]() sinA
sinA![]() ,整理得
,整理得![]() sinC﹣cosC=1,即sin(C
sinC﹣cosC=1,即sin(C![]() )
)![]() ,进而可得C的大小;
,进而可得C的大小;
(2)利用余弦定理可将cosB![]() 化成
化成![]() ,即8sinAcosB=5sinC=5sin
,即8sinAcosB=5sinC=5sin![]() ,进而求出sinAcosB的值.
,进而求出sinAcosB的值.
(1)△ABC中,![]() ,即cosA
,即cosA![]() sinA
sinA![]() ,
,
∴sinCcosA![]() sinAsinC=sinB+sinA,
sinAsinC=sinB+sinA,
∵sinB+sinA=sin(A+C)+sinA=sinAcosC+sinCcosA+sinA,
∴sinCcosA![]() sinAsinC=sinAcosC+sinCcosA+sinA,可得
sinAsinC=sinAcosC+sinCcosA+sinA,可得![]() sinAsinC=sinAcosC+sinA,
sinAsinC=sinAcosC+sinA,
∵sinA≠0,
∴![]() sinC﹣cosC=1,即sin(C
sinC﹣cosC=1,即sin(C![]() )
)![]() ,
,
∵C∈(0,π),C![]() ∈(
∈(![]() ,
,![]() ),
),
∴C![]() ,可得C
,可得C![]() .
.
(2)若![]() ,则cosB
,则cosB![]() ,即8sinAcosB=5sinC=5sin
,即8sinAcosB=5sinC=5sin![]() ,
,
所以sinAcosB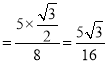 .
.

练习册系列答案
相关题目