题目内容
某单位建造一间背面靠墙的小房，地面为面积是12m2的矩形，房屋正面每平方米的造价为1200元，房屋侧面每平方米的造价为800元，屋顶的造价为6800元．如果墙高为3m，且不计房屋背面和地面的费用，问怎样设计房屋能使总造价最低？最低总造价是多少？
分析：如图所示，设底面的长为xm，宽ym，则y=
m．设房屋总造价为f（x），由题意可得f（x）=3x•1200+3×
×800×2+12×6800，利用基本不等式即可得出．
| 12 |
| x |
| 12 |
| x |
解答：解：如图所示，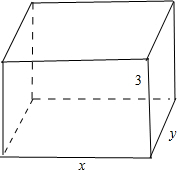
设底面的长为xm，宽ym，则y=
m．
设房屋总造价为f（x），
由题意可得f（x）=3x•1200+3×
×800×2+12×6800=3600x+
+81600
=3600×(x+
)+81600≥3600×2
+81600=110400，当且仅当x=4时取等号．
答：当底面的长宽分别为4m，3m时，可使房屋总造价最低，总造价是110400元．
设底面的长为xm，宽ym，则y=| 12 |
| x |
设房屋总造价为f（x），
由题意可得f（x）=3x•1200+3×
| 12 |
| x |
| 57600 |
| x |
=3600×(x+
| 16 |
| x |
x•
|
答：当底面的长宽分别为4m，3m时，可使房屋总造价最低，总造价是110400元．
点评：本题考查了利用基本不等式解决实际问题，属于中档题．
练习册系列答案
相关题目
某单位建造一间背面靠墙的房子，俯视图如图．地面面积为12m2，房屋正面每平方米的造价为1200元，房屋侧面每平方米的造价为800元，屋顶的造价共5200元．如果墙高为3m，且不计房屋背面和地面的造价．问怎样设计房屋能使总造价最低？最低总造价是多少？
，房屋正面每平方米的造价为
元，房屋侧面每平方米的造价为
元，屋顶的造价为
元．如果墙高为
m，且不计房屋背面和地面的费用，问怎样设计房屋能使总等价最低？最低总造价是多少？
