题目内容
(本小题满分13分) 已知椭圆C的对称中心为原点O,焦点在x轴上,左右焦点分别为 和
和 ,且|
,且|
 |=2,点(1,
|=2,点(1, )在该椭圆上.
)在该椭圆上.
(1)求椭圆C的方程;
(2)过 的直线
的直线 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 A
A B的面积为
B的面积为 ,求以
,求以 为圆心且与直线
为圆心且与直线 相切圆的方程.
相切圆的方程.
(1) ;(2)
;(2)
【解析】
试题分析:(1)椭圆C的方程为 ..(4分)
..(4分)
(2)①当直线l⊥x轴时,可得A(-1,- ),B(-1,
),B(-1, ),
), 的面积为3,不符合题
的面积为3,不符合题
意. (6分)
②当直线l与x轴不垂直时,设直线l的方程为y=k(x+1).代入椭圆方程得:
 ,显然△>0成立,设A
,显然△>0成立,设A ,则
,则
 ,可得|AB|=
,可得|AB|= ..(9分)
..(9分)
又圆 的半径r=
的半径r= ,∴
,∴ 的面积=
的面积= |AB| r=
|AB| r= ,化简得:
,化简得: ,
,
得k=±1,∴r = ,圆的方程为
,圆的方程为 ..(13分)
..(13分)
考点:本题考查椭圆的标准方程,直线与椭圆的位置关系,求圆方程,直线与圆的位置关系

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,且
,且 与
与 在直线
在直线 上的射影长度相等,直线
上的射影长度相等,直线 的倾斜角为锐角,则
的倾斜角为锐角,则 B.
B. C.
C. D.
D.
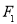 、
、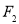 分别为双曲线
分别为双曲线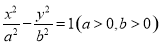 的左、右焦点.若在双曲线右支上存在点
的左、右焦点.若在双曲线右支上存在点 ,满足
,满足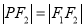 ,且
,且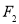 到直线
到直线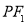 的距离等于双曲线的实轴长,则该双曲线的离心率为( )
的距离等于双曲线的实轴长,则该双曲线的离心率为( ) 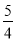 B.2 C.
B.2 C.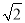 D.
D.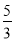
 与直线
与直线 互相垂直,那么
互相垂直,那么 的值等于 ( )
的值等于 ( ) C.
C. D.
D.
 有零点,则
有零点,则 的取值范围是
的取值范围是 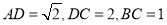 ,它可能随机在草原上任何一处(点),若落在扇形沼泽区域ADE以外丹顶鹤能生还,则该丹顶鹤生还的概率是( )
,它可能随机在草原上任何一处(点),若落在扇形沼泽区域ADE以外丹顶鹤能生还,则该丹顶鹤生还的概率是( )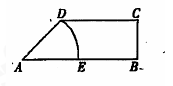
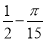 B.
B.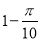 C.
C.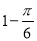 D.
D.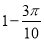
 ,则
,则 = .
= . 中,直线
中,直线 是曲线
是曲线 的切线,则当
的切线,则当 时,实数
时,实数 的最小值是
的最小值是