题目内容
如图,P是抛物线C:y=
x2上一点,直线l过点P且与抛物线C交于另一点Q.
(Ⅰ)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求
+
的取值范围.

| 1 |
| 2 |
(Ⅰ)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求
| |ST| |
| |SP| |
| |ST| |
| |SQ| |

(Ⅰ)设P(x1,y1),Q(x2,y2),M(x0,y0),依题意x1≠0,y1>0,y2>0.
由y=
x2,①
得y'=x.
∴过点P的切线的斜率k=x1,
∴直线l的斜率kl=-
=-
,
∴直线l的方程为y-
x12=-
(x-x1),②
联立①②消去y,得x2+
x-x12-2=0.
∵M是PQ的中点
∴x0=
=-
,y0=
x12-
(x0-x1)
消去x1,得y0=x02+
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+
+1(x≠0).
(Ⅱ)设直线l:y=kx+b,依题意k≠0,b≠0,则T(0,b).
分别过P、Q作PP'⊥x轴,QQ'⊥y轴,垂足分别为P'、Q',则
+
=
+
=
+
.
由y=
x2,y=kx+b消去x,得y2-2(k2+b)y+b2=0.③
则y1+y2=2(k2+b),y1y2=b2.
∴
+
=|b|(
+
)≥2|b|
=2|b|
=2.
∵y1、y2可取一切不相等的正数,
∴
+
的取值范围是(2,+∞).
由y=
| 1 |
| 2 |
得y'=x.
∴过点P的切线的斜率k=x1,
∴直线l的斜率kl=-
| 1 |
| k |
| 1 |
| x1 |
∴直线l的方程为y-
| 1 |
| 2 |
| 1 |
| x1 |
联立①②消去y,得x2+
| 2 |
| x1 |
∵M是PQ的中点
∴x0=
| x1+x2 |
| 2 |
| 1 |
| x1 |
| 1 |
| 2 |
| 1 |
| x1 |
消去x1,得y0=x02+
| 1 | ||
2
|
∴PQ中点M的轨迹方程为y=x2+
| 1 | ||
2
|
(Ⅱ)设直线l:y=kx+b,依题意k≠0,b≠0,则T(0,b).
分别过P、Q作PP'⊥x轴,QQ'⊥y轴,垂足分别为P'、Q',则
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
| |OT| |
| |P′P| |
| |OT| |
| |Q′Q| |
| |b| |
| |y1| |
| |b| |
| |y2| |
由y=
| 1 |
| 2 |
则y1+y2=2(k2+b),y1y2=b2.
∴
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
| 1 |
| y1 |
| 1 |
| y2 |
|
|
∵y1、y2可取一切不相等的正数,
∴
| |ST| |
| |SP| |
| |ST| |
| |SQ| |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,则椭圆的标准方程为( ).
,则椭圆的标准方程为( ).



 +
+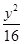 =1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,则下面结论正确的是( )
=1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,则下面结论正确的是( )