题目内容
已知函数![]() 其中
其中![]() 为大于零的常数。
为大于零的常数。
(1)若函数![]() 内调递增,求
内调递增,求![]() 的取值范围;
的取值范围;
(2)求函数![]() 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。
(3)求证:对于任意的![]() 成立
成立
(1)![]()
(2)![]() 在[1,2]上的最小值为
在[1,2]上的最小值为
①当![]()
②当![]() 时,
时,![]()
③当![]()
解析:
![]() ------------ 2分
------------ 2分
(1)由已知,得![]() 上恒成立,
上恒成立,
即![]() 上恒成立
上恒成立
又![]() 当
当![]()
![]() ------------ 4分
------------ 4分
(2)当![]() 时,
时,
![]() 在(1,2)上恒成立,
在(1,2)上恒成立,
这时![]() 在[1,2]上为增函数
在[1,2]上为增函数
![]()
当![]()
![]() 在(1,2)上恒成立,
在(1,2)上恒成立,
这时![]() 在[1,2]上为减函数 ------------6分
在[1,2]上为减函数 ------------6分
![]()
当![]() 时,
时,
令![]() ------------8分
------------8分
又![]()
![]()
![]() ------------ 9分
------------ 9分
综上,![]() 在[1,2]上的最小值为
在[1,2]上的最小值为
①当![]()
②当![]() 时,
时,![]()
③当![]() ------------ 10分
------------ 10分
(3)由(1),知函数![]() 上为增函数,
上为增函数,
当![]()
![]()
即![]()
![]()
![]()
![]() 恒成立 ------------ 14分
恒成立 ------------ 14分
![]() 恒成立 ------------ 12分
恒成立 ------------ 12分

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
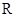 上的函数
上的函数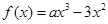 ,其中
,其中 为大于零的常数.
为大于零的常数.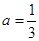 时,令
时,令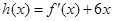 ,
,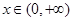 时,
时,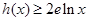 (
(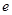 为自然对数的底数);
为自然对数的底数);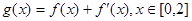 ,在
,在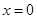 处取得最大值,求
处取得最大值,求