题目内容
已知定义在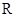 上的函数
上的函数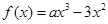 ,其中
,其中 为大于零的常数.
为大于零的常数.
(Ⅰ)当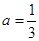 时,令
时,令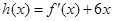 ,
,
求证:当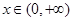 时,
时,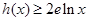 (
(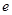 为自然对数的底数);
为自然对数的底数);
(Ⅱ)若函数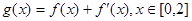 ,在
,在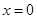 处取得最大值,求
处取得最大值,求 的取值范围
的取值范围
【答案】

所以
所以当 时,
时, 取得极小值,
取得极小值, 为
为 在
在 上的最小值
上的最小值
因为
所以 ,即
,即 -------------------6分
-------------------6分

当 时,
时, 为极小值,所以
为极小值,所以 在[0,2]上的最大值只能为
在[0,2]上的最大值只能为 或
或 ;
;
当 时,
时, 在
在 上单调递减,最大值为
上单调递减,最大值为 ,
,
所以 在
在 上的最大值只能为
上的最大值只能为 或
或 ;---------------11分
;---------------11分
又已知 在
在 处取得最大值,所以
处取得最大值,所以


即 解得
解得 ,所以
,所以
【解析】略

练习册系列答案
相关题目
 上的函数
上的函数 ,其中
,其中 为常数.
为常数. 是函数
是函数 的一个极值点,求
的一个极值点,求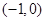 上是增函数,求实数
上是增函数,求实数 时,若
时,若 ,在
,在 处取得最大值,求实数
处取得最大值,求实数 上的函数
上的函数 ,则曲线
,则曲线 在点
在点 处的切线方程是( )
处的切线方程是( ) B.
B.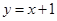 C.
C. D.
D.
 上的函数
上的函数 ,其中
,其中 为常数.
为常数. 是函数
是函数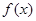 的一个极值点,求
的一个极值点,求 上是增函数,求
上是增函数,求 上的函数
上的函数 是奇函数且满足
是奇函数且满足 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 上的函数
上的函数 满足
满足 ,
, ,则不等式
,则不等式 的解集为
.
的解集为
.