题目内容
如图①,△BCD内接于直角梯形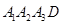 ,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.
,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.
(1)求证:AB⊥CD;
(2)求直线BD和平面ACD所成的角的正切值;
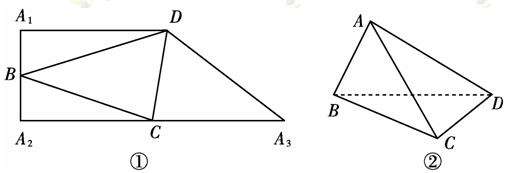
(3)求四面体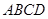 的体积。
的体积。
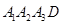 ,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.
,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.
(1)求证:AB⊥CD;
(2)求直线BD和平面ACD所成的角的正切值;
(3)求四面体
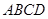 的体积。
的体积。(1)详见解析;(2)  ; (3)
; (3) 
 ; (3)
; (3) 
试题分析:(1)平面图中因为A1D∥A2A3,A1A2⊥A2A3,所以
 ,立体图中不变,即
,立体图中不变,即 ,可证得
,可证得 ,就可证出AB⊥CD。(2)由(1)知AB⊥平面ACD.,所以AD即为BD在面ACD内的射影,所以∠BDA即为所求。在直角三角形中利用三角函数可求其正切值。(3)由(1)知
,就可证出AB⊥CD。(2)由(1)知AB⊥平面ACD.,所以AD即为BD在面ACD内的射影,所以∠BDA即为所求。在直角三角形中利用三角函数可求其正切值。(3)由(1)知 ,所以可以选以面ADC为底面,以AB为高求其体积。
,所以可以选以面ADC为底面,以AB为高求其体积。试题解析:(1)证明:∵在直角梯形A1A2A3D中,A1B⊥A1D,A2B⊥A2C,
∴在三棱锥ABCD中,AB⊥AD,AB⊥AC.
∵AC∩AD=A,∴AB⊥平面ACD.
∵CD?平面ACD,∴AB⊥CD.
(2)解:由(1)知AB⊥平面ACD,
∴AD为BD在平面ACD内的射影,
∠BDA是直线BD和平面ACD所成的角.
依题意,在直角梯形A1A2A3D中,
A1D=A3D=10,A1B=A2B=4,
∴在三棱锥ABCD中,AD=10,AB=4.
在Rt△ABD中,tan ∠BDA=
 =
= =
= .
.∴直线BD和平面ACD所成的角的正切值为
 .
.(3)由(2)得:




练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
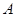 、
、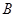 、
、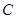 为不在同一直线上的三点,且
为不在同一直线上的三点,且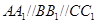 ,
,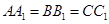 .
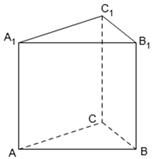
.
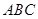 //平面
//平面 ;
;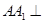 平面
平面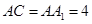 ,
,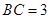 ,
,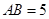 ,求证:
,求证: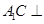 平面
平面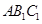 ;
;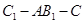 的余弦值.
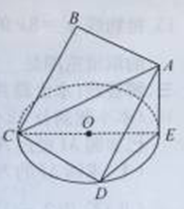
的余弦值.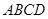 所在平面与圆
所在平面与圆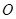 所在的平面相交于
所在的平面相交于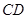 ,线段
,线段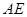 垂直于圆
垂直于圆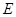 为圆
为圆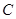 、
、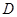 的点,设正方形
的点,设正方形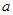 ,且
,且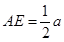 .
.
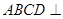 平面
平面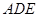 ;
;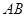 与
与 所成的角为
所成的角为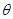 ,
,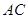 与底面
与底面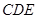 所成角为
所成角为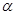 ,二面角
,二面角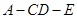 所成角为
所成角为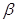 ,求证
,求证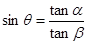
 中,已知
中,已知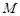 是棱
是棱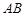 的中点.
的中点.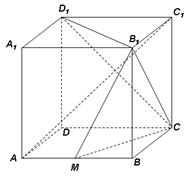
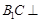 平面
平面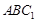 ,
,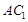 ∥平面
∥平面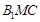 ;
;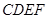 为正方形,平面
为正方形,平面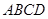 为等腰梯形,
为等腰梯形,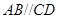 ,
,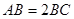 ,
,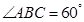 ,
, .
.
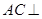 平面
平面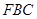 ;
;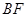 与平面
与平面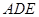 所成角的正弦值.
所成角的正弦值. 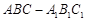 中,
中,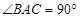 ,
,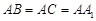 ,且
,且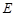 是
是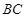 中点.
中点.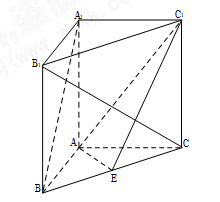
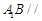 平面
平面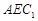 ;
;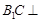 平面
平面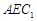 .
.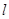 为直线,
为直线,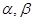 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )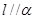 ,
, ,则
,则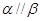
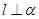 ,
,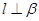 ,则
,则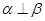 ,
,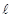 ⊥平面
⊥平面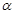 ,直线m
,直线m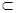 平面
平面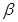 ,有下面四个命题:
,有下面四个命题: