题目内容
2．若0＜a＜1，函数f（x）=|logax|，则$f（\frac{1}{4}），f（\frac{1}{3}），f（2）$的大小关系为$f（2）＜f（\frac{1}{3}）＜f（\frac{1}{4}）$．分析 由题意可得f（$\frac{1}{4}$）=f（4），f（$\frac{1}{3}$）=f（3），由函数的单调性可得．
解答 解：∵0＜a＜1，函数f（x）=|logax|，
∴f（$\frac{1}{4}$）=|logax$\frac{1}{4}$|=|-loga4|=|loga4|=f（4），
同理可得f（$\frac{1}{3}$）=f（3），
又可得函数f（x）=|logax|在（1，+∞）单调递增，
∴$f（2）＜f（\frac{1}{3}）＜f（\frac{1}{4}）$，
故答案为：$f（2）＜f（\frac{1}{3}）＜f（\frac{1}{4}）$
点评 本题考查对数函数的图象和性质，涉及函数的单调性，属基础题．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
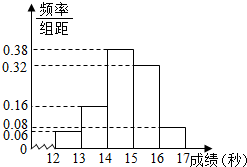某学校高三年级800名学生在一次百米测试中，成绩全部在12秒到17秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组[12，13），第二组[13，14），…，第五组[16，17]，如图是根据上述分组得到的频率分布直方图．