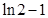题目内容
已知函数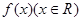 满足
满足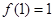 ,且
,且 的导函数
的导函数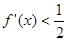 ,则
,则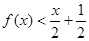 的解集为( )
的解集为( )
A.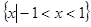 | B.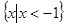 | C.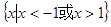 | D. |
D
解析试题分析:
设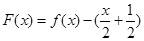 , 因为
, 因为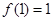 ,则
,则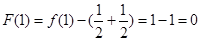 ,又因为
,又因为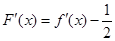 ,对任意
,对任意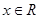 ,有
,有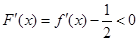 ,即函数
,即函数 在
在 上单调递减,则
上单调递减,则 的解集为
的解集为 ,即
,即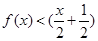 的解集为
的解集为 .
.
考点:1.函数导数的应用;2.构造函数思想.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
函数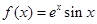 的图象在点
的图象在点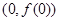 处的切线的倾斜角为( )
处的切线的倾斜角为( )
A. | B.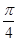 | C.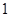 | D.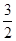 |
已知R上可导函数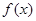 的图象如图所示,则不等式
的图象如图所示,则不等式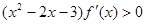 的解集为( )
的解集为( )
| A.(-∞,-2)∪(1,+∞) |
| B.(-∞,-2)∪(1,2) |
| C.(-∞,-1)∪(-1,0)∪(2,+∞) |
| D.(-∞,-1)∪(-1,1)∪(3,+∞) |
若曲线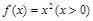 在点
在点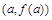 处的切线与两条坐标轴围成的三角形的面积为54,则
处的切线与两条坐标轴围成的三角形的面积为54,则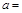 ( )
( )
| A.3 | B.6 | C.9 | D.18 |
设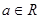 ,函数
,函数 的导函数为
的导函数为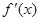 ,且
,且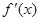 是奇函数,则
是奇函数,则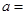 ( )
( )
| A.0 | B.1 | C.2 | D.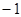 |
不等式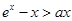 的解集为
的解集为 ,且
,且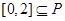 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A.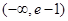 | B. | C.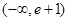 | D.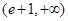 |
如果函数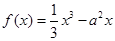 满足:对于任意的
满足:对于任意的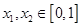 ,都有
,都有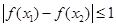 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( )
A. | B.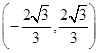 |
C. | D.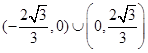 |
已知函数 的导函数为
的导函数为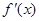 ,且满足
,且满足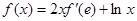 ,则
,则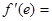 ( )
( )
A.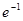 | B. | C. | D.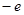 |
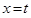 与函数
与函数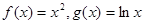 的图象分别交于点A、B,则|AB|的最小值为 ( )
的图象分别交于点A、B,则|AB|的最小值为 ( ) 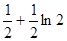 B.
B. C.
C. 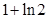 D.
D.