题目内容
(本题满分12分)一条双曲线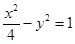 的左、右顶点分别为
的左、右顶点分别为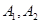 ,点
,点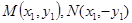 是双曲线上不同的两个动点。
是双曲线上不同的两个动点。
(1)求直线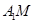 与
与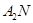 交点的轨迹
交点的轨迹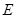 的方程式;
的方程式;
(2)设直线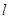 与曲线
与曲线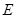 相交于不同的两点
相交于不同的两点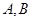 ,已知点
,已知点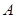 的
的 坐标为
坐标为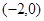 ,若点
,若点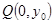 在线段
在线段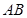 的垂直平分线上,且
的垂直平分线上,且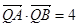 .求
.求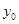 的值.
的值.
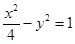 的左、右顶点分别为
的左、右顶点分别为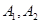 ,点
,点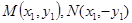 是双曲线上不同的两个动点。
是双曲线上不同的两个动点。(1)求直线
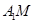 与
与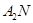 交点的轨迹
交点的轨迹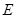 的方程式;
的方程式;(2)设直线
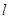 与曲线
与曲线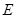 相交于不同的两点
相交于不同的两点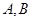 ,已知点
,已知点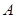 的
的 坐标为
坐标为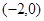 ,若点
,若点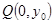 在线段
在线段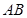 的垂直平分线上,且
的垂直平分线上,且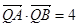 .求
.求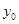 的值.
的值.解:(1)由 ,
, , ……………2分
, ……………2分
两式相乘得 ,而点
,而点 在双曲线上,
在双曲线上,
所以 ……………2分
……………2分
所以椭圆的方程为 . ….1分
. ….1分
(2)解:由(1)可知A(-2,0)。设B点的坐标为(x1,,y1),直线l的斜率为k,则直线l的方程为y=k(x+2),
于是A,B两点的坐标满足方程组
由方程组消去Y并整理,得 ……1分
……1分
由 得
得

设线段AB是中点为M,则M的坐标为 ……1分
……1分
(1)当k=0时,点B的坐标为(2,0)。线段AB的垂直平分线为y轴,于是
 …1分
…1分
(2)当K 时,线段AB的垂直平分线方程为
时,线段AB的垂直平分线方程为
令x=0,解得
由

 ……………2分
……………2分
整理得
综上
 ……2分
……2分
 ,
, , ……………2分
, ……………2分两式相乘得
 ,而点
,而点 在双曲线上,
在双曲线上,所以
 ……………2分
……………2分所以椭圆的方程为
 . ….1分
. ….1分(2)解:由(1)可知A(-2,0)。设B点的坐标为(x1,,y1),直线l的斜率为k,则直线l的方程为y=k(x+2),
于是A,B两点的坐标满足方程组

由方程组消去Y并整理,得
 ……1分
……1分由
 得
得
设线段AB是中点为M,则M的坐标为
 ……1分
……1分(1)当k=0时,点B的坐标为(2,0)。线段AB的垂直平分线为y轴,于是
 …1分
…1分(2)当K
 时,线段AB的垂直平分线方程为
时,线段AB的垂直平分线方程为
令x=0,解得

由


 ……………2分
……………2分整理得

综上

 ……2分
……2分略

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 右支上一点,
右支上一点, 分别为双曲线的左右焦点,且
分别为双曲线的左右焦点,且 ,I为三角形
,I为三角形 的内心,若
的内心,若 成立, 则
成立, 则 的值为( )
的值为( )



 ,且与椭圆
,且与椭圆 有相同的焦距,求双曲线的标准方程
有相同的焦距,求双曲线的标准方程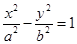 的左右焦点分别为
的左右焦点分别为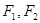 ,过
,过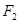 的直线交双曲线右支于
的直线交双曲线右支于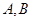 两点,且
两点,且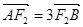 ,若
,若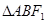 是以
是以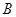 为顶角的等腰三角形,则双曲线的离心率等于( )
为顶角的等腰三角形,则双曲线的离心率等于( )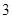
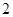
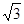
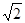
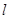 ,使得
,使得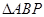 的面积最大时点P的坐标.
的面积最大时点P的坐标. 所截得的弦的中点,则直线l的方程是( )
所截得的弦的中点,则直线l的方程是( )



 的离心率为
的离心率为 ,则两条渐近线的方程为____
,则两条渐近线的方程为____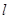 ,使得
,使得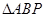 的面积最大时点P的坐标.
的面积最大时点P的坐标.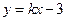 与双曲线
与双曲线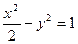 有且只有一个公共点,但直线与双曲线不相切,则实数
有且只有一个公共点,但直线与双曲线不相切,则实数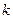 的值是
的值是