Question

已知△ABC顶点的直角坐标分别为A(3,4)、B(0,0)、C(c,0).

(1)(理(1)文(2))若c=5,求sin∠A的值;

(文)若=0,求c的值;

(2)(理)若∠A是钝角,求c的取值范围.

Answer 1

解:(1)(理(1)文(2))解法一:∵A(3,4)、B(0,0),

∴|AB|=5,sin∠B=.

当c=5时,|BC|=5,|AC|=

根据正弦定理,得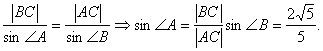

解法二:∵A(3,4)、B(0,0),

∴|AB|=5.

当c=5时,|BC|=5,|AC|=

根据余弦定理,得

cos∠A=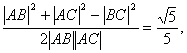

sin∠A=.

(文)解法一:∵A(3,4)、B(0,0)、C(c,0),

∴=(-3,-4),=(c-3,-4).

由·=0(-3)(c-3)+(-4)(-4)=0,

解得c=.

解法二:∵A(3,4)、B(0,0)、C(c,0),

∴|AB|²=3²+4²=25,|AC|²=(c-3)²+4²,|BC|²=c².

∵·=0,∴AB⊥AC,△ABC是直角三角形.

根据勾股定理,得|AB|²+|AC|²=|BC|²,

即c²=25+［(c-3)²+4²］.

解得c=.

(2)(理)已知△ABC顶点坐标为A(3,4)、B(0,0)、C(c,0),

∴|AC|²=(c-3)²+4²,|BC|²=c².

根据余弦定理,得cos∠A=,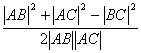

若∠A是钝角,则cos∠A＜0|AB|²+|AC|²-|BC|²＜0,

即5²+［(c-3)²+4²］-c²=50-6c＜0.

解得c＞.