题目内容
13.在1≤x≤2的条件下,求函数y=-x2+2ax+1(a是实常数)的最大值M和最小值m.分析 函数f(x)=-x2+2ax+1的图象的对称轴方程为x=a,通过讨论a的范围,得到函数的单调性,分别利用二次函数的性质求得f(x)在区间[1,2]上的最值.
解答 解:函数f(x)=-x2+2ax+1的图象的对称轴方程为x=a,
①当a<1时,f(x)在区间[1,2]上单调递减,
∴最小值为m=f(2)=4a-3,最大值为M=f(1)=2a.
②当1≤a<$\frac{3}{2}$时,
f(x)在[1,a)递增,在(a,2]递减,
可得最小值为m=f(2)=4a-3,最大值为M=f(a)=1+a2.
③当$\frac{3}{2}$≤a<2时,
f(x)在[1,a)递增,在(a,2]递减,
可得最小值为m=f(1)=2a,最大值为M=f(a)=1+a2.
④当a≥2时,f(x)在区间[1,2]上单调递增,
∴最大值为M=f(2)=4a-3,最小值为m=f(1)=2a.
点评 本题主要考查二次函数的性质的应用,体现了分类讨论、转化的数学思想,属中档题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
3.一个球体经过切割后,剩下部分几何体的三视图如图所示,则剩下部分几何体的体积为( )
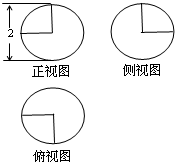

| A. | $\frac{7π}{6}$ | B. | $\frac{6π}{7}$ | C. | $\frac{4π}{3}$ | D. | $\frac{3π}{4}$ |
4.在兴趣小组的4名男生和3名女生中选取3人参加某竞赛,要求男生女生都至少有1人,则不同的选取方法有( )种.
| A. | 20 | B. | 30 | C. | 35 | D. | 60 |
5.在△ABC中,三个内角A,B,C的对边分别是a.b.c,已知B=30°,c=150,b=50$\sqrt{3}$,那么这个三角形是( )
| A. | 等边三角形 | B. | 等腰三角形 | ||
| C. | 直角三角形 | D. | 等腰三角或直角三角形 |