Question

【题目】已知不等式组 表示的平面区域为D，则
（1）z=x2+y2的最小值为 ．
（2）若函数y=|2x﹣1|+m的图象上存在区域D上的点，则实数m的取值范围是 ．

Answer 1

【答案】
（1）
（2）
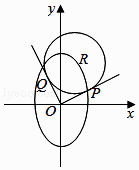
【解析】解：由题意作不等式组 平面区域如图：

1）z=x2+y2的最小值为图形中OP的距离的平方；

可得： = ．

2）结合图象可知， ，可得B（ ， ）， 解得A（2，﹣1）．当x∈[ ]时，

y=1+m﹣2x， 解得C（ ， ）

x∈（ ，2]时，y=2x﹣1+m，m的范围在A，B，C之间取得，y=|2x﹣1|+m，

经过A时，可得3+m=﹣1，即m=﹣4，m有最小值为﹣4；

经过C可得 ，可得m= ，即最大值为： ；

经过B可得1﹣ +m= ，m= ．

函数y=|2x﹣1|+m的图象上存在区域D上的点，则实数m的取值范围： ．

所以答案是： ， ．