题目内容
5.已知函数$f(x)=\left\{\begin{array}{l}\begin{array}{l}{{{log}_{\frac{1}{3}}}x,}&{x>1}\end{array}\\ \begin{array}{l}{-{x^2}-2x+4,}&{x≤1,}\end{array}\end{array}\right.$则f(f(3))=5; f(x)的单调递减区间是[-1,+∞).分析 求出f(3)的值,从而求出f(-1)的值,根据二次函数以及对数函数的性质求出函数的递减区间即可.
解答 解:f(3)=${log}_{\frac{1}{3}}^{3}$=-1,
∴f(f(3))=f(-1)=-1+2+4=5,
x≤1时,f(x)=-x2-2x+4=-(x+1)2+5,
对称轴x=-1,f(x)在[-1,1]递减,
x>1时,f(x)递减,
∴f(x)在[-1,+∞)递减,
故答案为:5;[-1,+∞).
点评 本题考查了求函数值问题,考查函数的单调性问题,是一道基础题.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
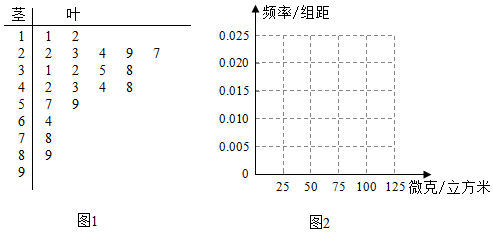
13.近期雾霾天气多发,对城市环境造成很大影响,某城市环保部门加强了对空气质量的监测.按国家环保部发布的(环境空气质量标准)规定,居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度的监测数据,数据记录如图1茎叶图
(1)完成如下的频率分布表,并在所给的坐标系(图2)中画出(0,100)的频率分布直方图;
(2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
(1)完成如下的频率分布表,并在所给的坐标系(图2)中画出(0,100)的频率分布直方图;
(2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | ||
| 第二组 | (25,50] | ||
| 第三组 | (50,75] | ||
| 第四组 | (75,100] |

20.函数f(x)的图象向左平移一个单位长度,所得的图象与函数y=2x的图象关于y轴对称,则f(x)=( )
| A. | y=2x-1 | B. | y=${(\frac{1}{2})^{x-1}}$ | C. | y=${(\frac{1}{2})^{x+1}}$ | D. | y=2x+1 |
15.已知函数f(x)=x2+4x,则f(2cosθ-1)的值域是( )
| A. | [-4,+∞) | B. | (-∞,-3] | C. | [-4,5] | D. | [-3,5] |
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)是偶函数,它的部分图象如图所示.M是函数f(x)图象上的点,K,L是函数f(x)的图象与x轴的交点,且△KLM为等腰直角三角形,则f(x)=$\frac{1}{2}$cosπx.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)是偶函数,它的部分图象如图所示.M是函数f(x)图象上的点,K,L是函数f(x)的图象与x轴的交点,且△KLM为等腰直角三角形,则f(x)=$\frac{1}{2}$cosπx.