题目内容
已知函数![]() =
=![]() (a
(a![]() R).
R).
(1)当![]() 时,证明函数
时,证明函数![]() 只有一个零点;
只有一个零点;
(2)若函数![]() 在区间(1,+
在区间(1,+![]() )上是减函数,求实数a的取值范围.
)上是减函数,求实数a的取值范围.
解:(1)当![]() ,其定义域是(0,+
,其定义域是(0,+![]() )
)
∴![]()
令![]()
∵x>0
∴![]() 舍去
舍去
当0<x<1时,![]()
∴函数![]() 上单调递增,在区间(1,+
上单调递增,在区间(1,+![]() )上单调递减。
)上单调递减。
当x=1时,![]() 的取得最大值,其值为
的取得最大值,其值为![]()
当![]() 时,
时,![]()
∴函数![]() 只有一个零点。
只有一个零点。
(2)因为![]() 其定义域为(0,+
其定义域为(0,+![]() )
)
所以![]()
![]()
![]()
①当![]()
∴![]() 上为增函数,不合题意。
上为增函数,不合题意。
②当a>0时,![]()
即![]()
此时![]()
依题意,得![]()
解之得![]()
③当a<0时,![]()
即![]()
此时![]()
依题意,得
解之得解之得![]()
综上所述,实数a 的取值范围是![]() .
.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
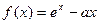 (
(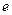 为自然对数的底数).a
为自然对数的底数).a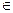 R
R 1)当a=1时,求函数
1)当a=1时,求函数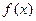 的最小值;
的最小值;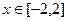 上存在极小值,求a的取值范围;
上存在极小值,求a的取值范围;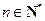 ,证明:
,证明: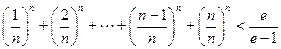 .
. R).
R). )上是增函数,求实数a的取值范围;
)上是增函数,求实数a的取值范围; ,且f(x0)=3,求x0的值;
,且f(x0)=3,求x0的值; ,且在R上是减函数,求实数a的取值范围。
,且在R上是减函数,求实数a的取值范围。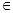 R).
R). )上是增函数,求实数a的取值范围;
)上是增函数,求实数a的取值范围;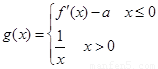 ,且f(x0)=3,求x0的值;
,且f(x0)=3,求x0的值;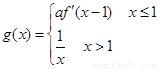 ,且在R上是减函数,求实数a的取值范围。
,且在R上是减函数,求实数a的取值范围。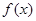 =
=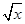 ,
,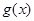 =alnx,a
=alnx,a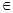 R。
R。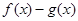 ,当h(x)存在最小之时,求其最小值
,当h(x)存在最小之时,求其最小值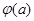 的解析式;
的解析式;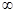 )时,
)时,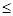 1.
1.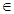 R)
且
R)
且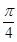 是函数Y=f(X)的零点
是函数Y=f(X)的零点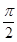 〕,求函数f(X)的值域
〕,求函数f(X)的值域