题目内容
已知函数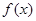 =
=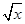 ,
,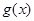 =alnx,a
=alnx,a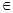 R。
R。
(1)
若曲线y=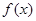 与曲线y=
与曲线y=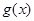 相交,且在交点处有相同的切线,求a的值及该切线的方程;
相交,且在交点处有相同的切线,求a的值及该切线的方程;
(2)设函数h(x)= 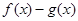 ,当h(x)存在最小之时,求其最小值
,当h(x)存在最小之时,求其最小值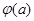 的解析式;
的解析式;
(3)对(2)中的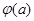 ,证明:当a
,证明:当a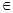 (0,+
(0,+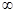 )时,
)时,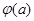
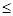 1.
1.
【答案】
因为两曲线在交点处有相同切线,所以两函数在交点处的导数相等
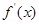 =
=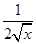 ,g’(x)=
,g’(x)= 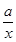 , 令f’(x)=g’(x)得
, 令f’(x)=g’(x)得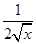 =
=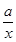 ,代入原函数,令f(x)=g(x)解得x=
,代入原函数,令f(x)=g(x)解得x=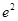
所以交点坐标为(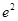 ,e),该点导数即斜率为
,e),该点导数即斜率为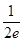 , 切线:y-e=
, 切线:y-e=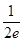 ·(x-
·(x-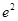 )
)
即
y=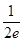 x+
x+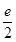
(2)函数h(x)=
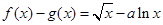 ,
,
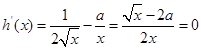 ,
,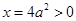
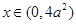 ,h(x)为减函数,
,h(x)为减函数,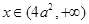 ,h(x)为增函数,
,h(x)为增函数,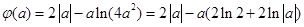
(3)当a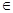 (0,+
(0,+ )时,
)时,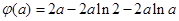 ,
,
 ,
,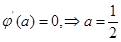 ,
,
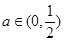 ,
,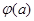 为增函数,
为增函数,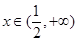 ,
,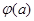 为减增函数,则
为减增函数,则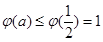
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目