题目内容

已知函数f(x)=x3+ax-2,(a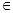R).

(l)若f(x)在区间(1,+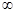)上是增函数，求实数a的取值范围;

(2)若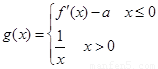，且f(x0)=3，求x0的值；

(3)若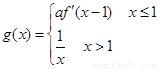，且在R上是减函数，求实数a的取值范围。

 

【答案】

（1）的取值范围是；（2），或（3）.

【解析】

试题分析：（1）求导得：，因为在区间上是增函数，所以在上恒成立，即恒成立，只需大于等于的最大值即可；

（2），即.分段函数求值就分情况分别求.

（3）即在上是减函数，则两段都递减且时两段的端点重合，由此即可求出的取值范围.

试题解析：（1），在区间上是增函数，所以，在上恒成立，恒成立，所以，的取值范围是         4分

（2）即

由，即或

所以，或.          9分

（3）即在上是减函数，所以

解之得.        13分

考点：1、函数的单调性及函数的值；2、分段函数.

 

练习册系列答案
相关题目
已知函数f(x)=x-2m2+m+3(m∈Z)为偶函数，且f（3）＜f（5）．
（1）求m的值，并确定f（x）的解析式；
（2）若g（x）=loga[f（x）-ax]（a＞0且a≠1），是否存在实数a，使g（x）在区间[2，3]上的最大值为2，若存在，请求出a的值，若不存在，请说明理由．
（2011•上海模拟）已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．

已知函数f(x)的图像在[a，b]上连续不断，f1(x)＝min{f(t)|a≤t≤x}(x∈[a，b])，f2(x)＝max{f(t)|a≤t≤x}(x∈[a，b])，其中，min{f(x)|x∈D}表示函数f(x)在D上的最小值，max{f(x)|x∈D}表示函数f(x)在D上的最大值，若存在最小正整数k，使得f2(x)－f1(x)≤k(x－a)对任意的x∈[a，b]成立，则称函数f(x)为[a，b]上的“k阶收缩函数”．已知函数f(x)＝x2，x∈[－1，4]为[－1，4]上的“k阶收缩函数”，则k的值是_________．
已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f（x）、g（x），下列说法正确的是（ ）
A．f（x）是奇函数，g（x）是奇函数，则f（x）+g（x）是奇函数
B．f（x）是偶函数，g（x）是偶函数，则f（x）+g（x）是偶函数
C．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）一定是奇函数或偶函数
D．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）可以是奇函数或偶函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网