题目内容
设F1,F2是椭圆C:
+
=1(a>b>0)的两个焦点,若在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
分析:根据已知条件,利用椭圆的性质推导出|PF1|=2a-c,|PF2|=c,|F1F2|=2c,∠F1PF2=90°,由此利用勾股定理能求出椭圆的离心率.
解答:解:∵F1,F2是椭圆C:
+
=1(a>b>0)的两个焦点,
在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,
∴|PF1|=2a-c,|PF2|=c,|F1F2|=2c,∠F1PF2=90°,
∴(2a-c)2+c2=4c2,
整理,得2a2-2ac=c2,
∴e2+2e-2=0,
解得e=
-1,或e=-1-
(舍)
故答案为:
-1.
| x2 |
| a2 |
| y2 |
| b2 |
在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,
∴|PF1|=2a-c,|PF2|=c,|F1F2|=2c,∠F1PF2=90°,
∴(2a-c)2+c2=4c2,
整理,得2a2-2ac=c2,
∴e2+2e-2=0,
解得e=
| 3 |
| 3 |
故答案为:
| 3 |
点评:本题考查椭圆的离心率的求法,解题时要认真审题,注意勾股定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011•浙江模拟)设F1,F2是椭圆C:
(2011•浙江模拟)设F1,F2是椭圆C: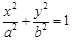 (a>b>0)的左、右焦点,过F1的直线
(a>b>0)的左、右焦点,过F1的直线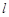 与
与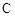 交于A,B两点.若AB⊥AF2,|AB|:|AF2|=3:4,则椭圆的离心率为
.
交于A,B两点.若AB⊥AF2,|AB|:|AF2|=3:4,则椭圆的离心率为
.