题目内容
已知命题![]() 和
和![]() 是方程
是方程![]() 的两个实根,不等式
的两个实根,不等式![]() 对任意实数
对任意实数![]() 恒成立;命题
恒成立;命题![]() 不等式
不等式![]() 有解;若命题
有解;若命题![]() 是真命题,命题
是真命题,命题![]() 是假命题,求
是假命题,求![]() 的取值范围。
的取值范围。
解:![]() 、
、![]() 是方程
是方程![]() 的两个实根
的两个实根

![]()
∴当![]() 时,
时,![]()
由不等式![]() 对任意实数
对任意实数![]() 恒成立可得:
恒成立可得:
![]()
![]() 或
或![]()
∴命题![]() 为真命题时
为真命题时![]() 或
或![]()
命题![]() 不等式
不等式![]() 有解
有解
①当![]() 时,显然有解
时,显然有解
②当![]() 时,
时,![]() 有解
有解
③当![]() 时,
时,![]() 有解
有解
![]()
![]()
从而命题![]() 不等式
不等式![]() 有解时
有解时![]()
又命题![]() 是假命题
是假命题
![]()
故命题![]() 是真假题且命题
是真假题且命题![]() 是假命题时,
是假命题时,![]() 的取值范围为
的取值范围为
![]()

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
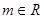 ,对
,对 :
: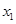 和
和 是方程
是方程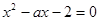 的两个根,不等式
的两个根,不等式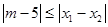 对任意实数
对任意实数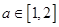 恒成立;
恒成立;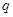 :函数
:函数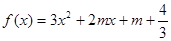 有两个零点,求使“
有两个零点,求使“
 和
和 是方程
是方程 的两个实根,不等式
的两个实根,不等式 对任意实数
对任意实数 恒成立;命题
恒成立;命题 只有一个实数
只有一个实数 满足不等式
满足不等式 ,若命题
,若命题 是假命题,命题
是假命题,命题 是真命题,求
是真命题,求 的取值范围。
的取值范围。