题目内容

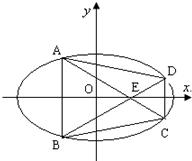如图，椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)过点M（1，
4
2
3
），N（
3
3
2
，1），梯形ABCD（AB∥CD∥y轴，且AB＞CD）内接于椭圆，E是对角线AC与BD的交点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设AB=m，CD=n，OE=d，试求
m-n
d
的最大值．
分析：（Ⅰ）把M、N两点坐标代入椭圆方程解方程组即可；
（Ⅱ）易判断点E在x轴上，则E（d，0），设BD的方程为x=ky+d（k＞0），与椭圆方程联立消x得关于y的一元二次方程，设B（x1，y1），D（x2，y2），由韦达定理可得y1+y2，进而可把m-n、
m-n
d
用k表示出来，再利用基本不等式即可求得其最大值．
解答：解：（Ⅰ）由题意得
27
4a2
+
1
b2
=1
1
a2
+
32
9b2
=1
，
解得a2=9，b2=4，
所以椭圆C的方程为：
x2
9
+
y2
4
=1．
（Ⅱ）根据对称性可知点E在x轴上，则E点的坐标为（d，0），
设BD的方程为x=ky+d（k＞0），由
x=ky+d
x2
9
+
y2
4
=1
得（9+4k2）y2+8dky+4d2-36=0，
设B（x1，y1），D（x2，y2），则y1+y2=-
8dk
9+4k2
，
m-n=-2y1-2y2=
16dk
9+4k2
，
从而
m-n
d
=
16k
9+4k2
≤
16k
2
9×4k2
=
16k
12k
=
4
3
，
等号当且仅当k=
3
2
取得．
m-n
d
的最大值为
4
3
．
点评：本题考查直线与圆锥曲线的综合问题及椭圆方程的求解，考查基本不等式在求最值中的应用，考查学生综合运用知识分析解决问题的能力，（Ⅱ）问关键是
m-n
d
表示为k的函数．
练习册系列答案
相关题目
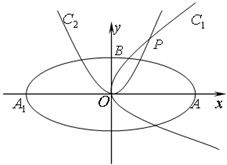精英家教网如图，椭圆C：
x2
a2
+
y2
2
=1焦点在x轴上，左、右顶点分别为A1、A，上顶点为B，抛物线C1、C2分别以A、B为焦点，其顶点均为坐标原点O．C1与C2相交于直线y=
2
x上一点P．
（Ⅰ）求椭圆C及抛物线C1、C2的方程；
（Ⅱ）若动直线l与直线OP垂直，且与椭圆C交于不同两点M、N，已知点Q(-
2
，0），求
QM
.
QN
的最小值．
（2008•闸北区二模）如图，椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，A1、A2为椭圆C的左、右顶点．
（Ⅰ）设F1为椭圆C的左焦点，证明：当且仅当椭圆C上的点P在椭圆的左、右顶点时|PF1|取得最小值与最大值；
（Ⅱ）若椭圆C上的点到焦点距离的最大值为3，最小值为1．求椭圆C的标准方程；
（Ⅲ）若直线l：y=kx+m与（Ⅱ）中所述椭圆C相交于A，B两点（A，B不是左右顶点），且满足AA2⊥BA2，求证：直线l过定点，并求出该定点的坐标．
如图，椭圆C：
x2
a2
+
y2
a2-1
=1的左右顶点分别为A、B，左右焦点分别为F1、F2，P为以F1、F2为直径的圆上异于F1、F2的动点，直线PF1、PF2分别交椭圆C于M、N和D、E．
（1）证明：
AP
•
BP
为定值K；
（2）当K=-2时，问是否存在点P，使得四边形DMEN的面积最小，若存在，求出最小值和P坐标，若不存在，请说明理由．
如图，椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的顶点为A1、A2、B1、B2，焦点为F1，
F2，|A1B1|=
7
，
S?A1B1A2B 2=2S?B1F1B2F 2
（1）求椭圆C的方程；
（2）设l是过原点的直线，直线n与l垂直相交于P点，且n与椭圆相交于A，B两点，|OP|=1，求
AP
•
PB
的取值范围．
（2011•重庆三模）光线被曲线反射，等效于被曲线在反射点处的切线反射．已知光线从椭圆的一个焦点出发，被椭圆反射后要回到椭圆的另一个焦点；光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出；如图，椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)与双曲线C′：
x2
m2
-
y2
n2
=1(m＞0，n＞0)有公共焦点，现一光线从它们的左焦点出发，在椭圆与双曲线间连续反射，则光线经过2k（k∈N*）次反射后回到左焦点所经过的路径长为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网