题目内容
已知曲线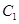 的参数方程是
的参数方程是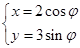 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线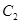 的极坐标方程是ρ=2,正方形ABCD的顶点都在
的极坐标方程是ρ=2,正方形ABCD的顶点都在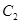 上,且A,B,C,D依逆时针次序排列,点A的极坐标为
上,且A,B,C,D依逆时针次序排列,点A的极坐标为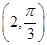 .
.
(Ⅰ)求点A,B,C,D的直角坐标;
(Ⅱ)设P为 上任意一点,求
上任意一点,求 的取值范围.
的取值范围.
(Ⅰ)A(1, ),B(-
),B(- ,1),C(-1,-
,1),C(-1,- ),D(
),D( ,-1);(Ⅱ)
,-1);(Ⅱ) 的取值范围是[32,52]
的取值范围是[32,52]
解析试题分析:(Ⅰ)根据已知条件可得A(2cos ,2sin
,2sin ),B(2cos(
),B(2cos( +
+ ),2sin(
),2sin( +
+ )),C(2cos(
)),C(2cos( +π),2sin(
+π),2sin( +π)),D(2cos(
+π)),D(2cos( +
+ ),2sin(
),2sin( +
+ )),然后将其化为直角坐标即可;(Ⅱ)设P(2cosφ,3sinφ),令S=
)),然后将其化为直角坐标即可;(Ⅱ)设P(2cosφ,3sinφ),令S= ,利用三角函数求解.
,利用三角函数求解.
试题解析: (1)由已知可得A(2cos ,2sin
,2sin ),B(2cos(
),B(2cos( +
+ ),2sin(
),2sin( +
+ )),
)),
C(2cos( +π),2sin(
+π),2sin( +π)),D(2cos(
+π)),D(2cos( +
+ ),2sin(
),2sin( +
+ )),4分
)),4分
即A(1, ),B(-
),B(- ,1),C(-1,-
,1),C(-1,- ),D(
),D( ,-1). 5分
,-1). 5分
(2)设P(2cosφ,3sinφ),令S= ,
,
则S=16cos2φ+36sin2φ+16=32+20sin2φ. 9分
因为0≤sin2φ≤1,所以S的取值范围是[32,52]. 10分
考点:极坐标和参数方程、三角函数、直角坐标和极坐标互化.

练习册系列答案
相关题目
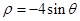 和
和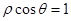 相交于点
相交于点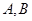 ,则线段
,则线段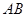 的长度为 .
的长度为 . 的极坐标方程是
的极坐标方程是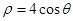 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (
( 是参数).若直线
是参数).若直线 的值.
的值. 的参数方程为
的参数方程为 (
(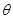 为参数),曲线
为参数),曲线 的极坐标方程
的极坐标方程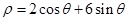 .
.  中,曲线
中,曲线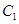 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,得曲线
轴的非负半轴为极轴建立极坐标系,得曲线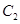 的极坐标方程为
的极坐标方程为 (
( )
)  :
:  (
( 为参数)过曲线
为参数)过曲线 轴负半轴的交点,求与直线
轴负半轴的交点,求与直线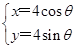 (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为 .
.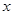 轴的非负半轴为极轴建立坐标系.已知点
轴的非负半轴为极轴建立坐标系.已知点 的极坐标为
的极坐标为 ,直线的极坐标方程为
,直线的极坐标方程为 ,且点
,且点 的值及直线的直角坐标方程;
的值及直线的直角坐标方程; ,(
,( 为参数),试判断直线与圆的位置关系.
为参数),试判断直线与圆的位置关系.  中,已知曲线
中,已知曲线 ,以平面直角坐标系
,以平面直角坐标系 为极点,
为极点, 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线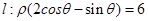 .
. 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 、
、 倍后得到曲线
倍后得到曲线 ,试写出直线的直角坐标方程和曲线
,试写出直线的直角坐标方程和曲线 ,使点
,使点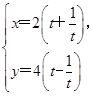 (t为参数)化为普通方程.
(t为参数)化为普通方程.