题目内容
在平面直角坐标系中,以坐标原点为极点,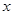 轴的非负半轴为极轴建立坐标系.已知点
轴的非负半轴为极轴建立坐标系.已知点 的极坐标为
的极坐标为 ,直线的极坐标方程为
,直线的极坐标方程为 ,且点
,且点 在直线上.
在直线上.
(1)求 的值及直线的直角坐标方程;
的值及直线的直角坐标方程;
(2)圆c的参数方程为 ,(
,( 为参数),试判断直线与圆的位置关系.
为参数),试判断直线与圆的位置关系.
(1) ,
,
(2)相交
解析试题分析:解:(Ⅰ)由点 在直线
在直线 上,可得
上,可得
所以直线的方程可化为
从而直线的直角坐标方程为 5分
5分
(Ⅱ)由已知得圆 的直角坐标方程为
的直角坐标方程为
所以圆心为 ,半径
,半径
以为圆心到直线的距离 ,所以直线与圆相交 10分
,所以直线与圆相交 10分
考点:直线与圆的位置关系
点评:主要是考查了直线与圆的位置关系的运用,属于基础题。

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是 ( )
A. =-10x+200 =-10x+200 | B. =10x+200 =10x+200 |
C. =-10x-200 =-10x-200 | D. =10x-200 =10x-200 |
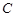 的参数方程为
的参数方程为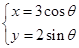 (
(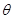 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线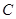 上的点按坐标变换
上的点按坐标变换 得到曲线
得到曲线 .
. 在曲线
在曲线
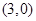 ,当点
,当点 中点
中点 的轨迹方程.
的轨迹方程.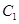 的参数方程是
的参数方程是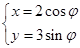 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线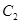 的极坐标方程是ρ=2,正方形ABCD的顶点都在
的极坐标方程是ρ=2,正方形ABCD的顶点都在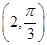 .
. 的取值范围.
的取值范围. 的参数方程为
的参数方程为
 是参数
是参数 ,
, 是曲线
是曲线 轴正半轴的交点.以坐标原点
轴正半轴的交点.以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 的极坐标方程.
的极坐标方程. 的参数方程为
的参数方程为 (
( 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
. 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,x轴的正半轴为极轴建立极坐标系,圆
为极点,x轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.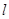 经过点
经过点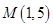 ,倾斜角是
,倾斜角是
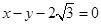 的交点与点
的交点与点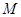 的距离
的距离 :
: 上找一点
上找一点 使点
使点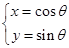 (
(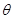 为参数,
为参数,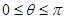 )上的点,点A的坐标为(1,0),
)上的点,点A的坐标为(1,0),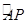 的长度均为
的长度均为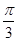 。
。 轴的正半轴为极轴建立极坐标系,求点M的极坐标;
轴的正半轴为极轴建立极坐标系,求点M的极坐标;