题目内容
甲、乙两射手在同一条件下进行射击,分布列如下:射手甲击中环数8,9,10的概率分别为0.2,0.6,0.2;射手乙击中环数8,9,10的概率分别为0.4,0.2,0.4.用击中环数的期望与方差比较两名射手的射击水平.
解:Eξ1=8×0.2+9×0.6+10×0.2=9,
V(ξ1)=(8-9)2×0.2+(9-9)2×0.6+(10-9)2×0.2=0.4;
同理有E(ξ2)=9,V(ξ2)=0.8.
由上可知,E(ξ1)=E(ξ2),V(ξ1)<V(ξ2).所以,在射击之前,可以预测甲、乙两名射手所得的平均环数很接近,均在9环左右,但甲所得环数较集中,以9环居多,而乙得环数较分散,得8、10环的次数多些.

练习册系列答案
相关题目
下表中有三个游戏规则,袋子中分别装有大小相同的球,从袋子中取球,分别计算甲获胜的概率,说明哪个游戏是公平的?
| 游戏1 | 游戏2 | 游戏3 |
| 1个红球和1个白球 | 2个红球和2个白球 | 3个红球和1个白球 |
| 取1个球 | 取1个球,再取1个球 | 取1个球,再取1个球 |
| 取出的球是红球→甲胜 | 取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
| 取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
分析:游戏是否公平的关键是看甲、乙获胜的概率是否相等.
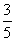
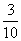
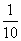
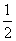 ,且各件产品是否为优质品相互独立.
,且各件产品是否为优质品相互独立. ,则λ=________.
,则λ=________.