题目内容
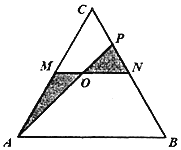
【题目】交大设计学院植物园准备用一块边长为4百米的等边ΔABC田地(如图)建立芳香植物生长区、植物精油提炼处与植物精油体验点.田地内拟建笔直小路MN、AP,其中M、N分别为AC、BC的中点,点P在CN上.规划在小路MN和AP的交点O(O与M、N不重合)处设立植物精油体验点,图中阴影部分为植物精油提炼处,空白部分为芳香植物生长区,A、N为出入口(小路宽度不计).为节约资金,小路MO段与OP段建便道,供芳香植物培育之用,费用忽略不计,为车辆安全出入,小路AO段的建造费用为每百米4万元,小路ON段的建造费用为每百米3万元.
(1)若拟建的小路AO段长为![]() 百米,求小路ON段的建造费用;
百米,求小路ON段的建造费用;
(2)设∠BAP=![]() ,求
,求![]() 的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
【答案】(1) 小路ON段的建造费用为3万元.
(2) 当![]() 时,小路AO段与ON段的建造总费用最小,最小费用约为
时,小路AO段与ON段的建造总费用最小,最小费用约为![]() 元.
元.
【解析】
(1) 在△ ![]() 中,
中,![]() ,
,![]() ,∠
,∠![]() ,利用余弦定理可求解
,利用余弦定理可求解![]() 长度,结合
长度,结合![]() 即可求解;
即可求解;
(2)在△ ![]() 中,
中,![]() ,∠
,∠![]() ,
,![]() ,
,![]() ,利用正弦定理可求
,利用正弦定理可求![]() ,结合
,结合![]() ,可建立关于
,可建立关于![]() 的函数,利用导数即可判断最值.
的函数,利用导数即可判断最值.
(1)由![]() 为
为![]() 中点,得
中点,得![]() ,在△
,在△ ![]() 中,∠
中,∠![]() ,由余弦定理可得,
,由余弦定理可得,![]() ,解得
,解得![]() 或-3(舍去),又
或-3(舍去),又![]() ,所以
,所以![]() ,故小路ON段的建造费用为3万元.
,故小路ON段的建造费用为3万元.
(2)在△ ![]() 中,∠
中,∠![]() ,
,![]() ,由正弦定理可得,
,由正弦定理可得,![]() ,即
,即![]() ,
, 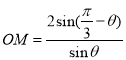 ,故小路AO段与ON段的建造总费用为
,故小路AO段与ON段的建造总费用为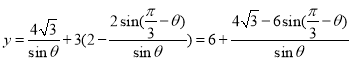
![]() ,
,
则![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,故当
,故当![]() 时,小路AO段与ON段的建造总费用最小,由
时,小路AO段与ON段的建造总费用最小,由![]() ,得
,得![]() ,故最小费用为
,故最小费用为![]() 元.
元.

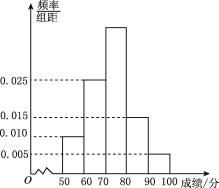
【题目】我校对高二600名学生进行了一次知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
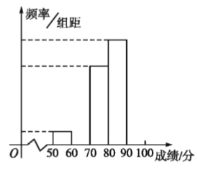
(1)填写频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
分组 | 频数 | 频率 |
| 2 | 0.04 |
| 8 | 0.16 |
| 10 | ________ |
| ________ | ________ |
| 14 | 0.28 |
合计 | ________ | 1.00 |
(2)请你估算该年级学生成绩的中位数;
(3)如果用分层抽样的方法从样本分数在![]() 和
和![]() 的人中共抽取6人,再从6人中选2人,求2人分数都在
的人中共抽取6人,再从6人中选2人,求2人分数都在![]() 的概率.
的概率.