Question

（09年长郡中学一模文）（13分）

已知圆，定点,点为圆上的动点，点在上，点

在上，且满足

（I）求点的轨迹的方程；

（II）过点作直线，与曲线交于,两点，是坐标原点，设 是否存在这样的直线，使四边形的对角线相等（即）？若存在，求出直线的方程；若不存在，试说明理由.  

Answer 1

解析：（I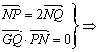）Q为PN的中点且GQ⊥PNGQ为PN的中垂线|PG|=|GN|  

∴|GN|+|GM|=|MP|=6，故G点的轨迹是以M、N为焦点的椭圆，

其长半轴长，半焦距，∴短半轴长b=2，

∴点G的轨迹方程是 ………5分

   (Ⅱ)因为，所以四边形OASB为平行四边形

       若存在l使得||=||，则四边形OASB为矩形

       若l的斜率不存在，直线l的方程为x=2，由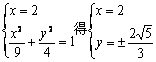

       矛盾，故l的斜率存在.    ………7分

       设l的方程为

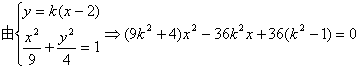          ………9分

          ①             ………10分

   ② 

       把①、②代入             ………12分

  ∴存在直线使得四边形OASB的对角线相等.  13分