题目内容
(09年长郡中学一模文)(12分)
如图,四面体ABCD中,O、E分别是BD、BC的中点,
![]()
(I)求证:![]() 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的余弦;
(III)求点E到平面ACD的距离.

解析:方法一:
(I)证明:连结OC
![]() ………1分
………1分
![]()
在![]() 中,由已知可得
中,由已知可得![]()
而![]()
![]()
![]() 即
即![]() ……………3分
……………3分
又![]()
![]() 平面
平面![]() ……………4分
……………4分
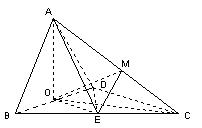
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知![]()
![]() 直线OE与EM所成的锐角就是异面直线AB与CD所成的角。……………5分
直线OE与EM所成的锐角就是异面直线AB与CD所成的角。……………5分
在![]() 中,
中,
![]() ……………6分
……………6分
![]() 是直角
是直角![]() 斜边AC上的中线,
斜边AC上的中线,
![]() ……………7分
……………7分
![]()
![]() 异面直线AB与CD所成角大小的余弦为
异面直线AB与CD所成角大小的余弦为![]() ;……………8分
;……………8分
(III)解:设点E到平面ACD的距离为![]()
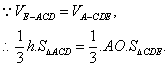 ……………9分
……………9分
在![]() 中,
中,![]()
![]() ……………10分
……………10分
而![]() ……………11分
……………11分
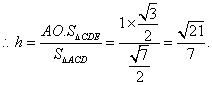
![]() 点E到平面ACD的距离为
点E到平面ACD的距离为![]() ……………12分
……………12分
方法二:
(I)同方法一.……………4分
(II)解:以O为原点,如图建立空间直角坐标系,

则![]()
![]() ………………6分
………………6分
![]() …………7分
…………7分
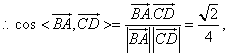 ………9分
………9分
![]() 异面直线AB与CD所成角大小的余弦为
异面直线AB与CD所成角大小的余弦为![]() ;……………8分
;……………8分
(III)解:设平面ACD的法向量为![]() 则
则
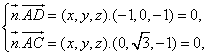 ……………9分
……………9分
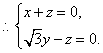
令![]() 得
得![]() 是平面ACD的一个法向量.……………10分
是平面ACD的一个法向量.……………10分
又![]()
![]() 点E到平面ACD的距离
点E到平面ACD的距离
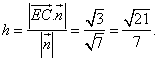 ……………12分
……………12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,写出
,写出