题目内容
如图，半径为R的半球内有一内接正六棱锥P-ABCDEF，则直线PA与平面BPE所成角正弦值是 ．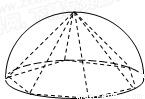
【答案】分析：设点P在平面ABCDEF内的射影为点O，过点A作BE的垂线，垂足为Q，连接PQ，则∠APQ为直线PA与平面BPE所成角，在直角三角形APQ中求解此角即可．
解答：
解：如图
设点P在平面ABCDEF内的射影为点O，过点A作BE的垂线，垂足为Q，连接PQ
∵AQ⊥QE，而PO⊥AQ，PO∩QE=Q
∴AQ⊥面BPE
∴∠APQ为直线PA与平面BPE所成角
在Rt△APQ中，AP=
，AQ=
∴
，
故答案为
点评：本题主要考查了直线与平面的所成角，以及解三角形等知识，考查空间想象能力、运算能力和推理论证能力，属于基础题．
解答：
解：如图设点P在平面ABCDEF内的射影为点O，过点A作BE的垂线，垂足为Q，连接PQ
∵AQ⊥QE，而PO⊥AQ，PO∩QE=Q
∴AQ⊥面BPE
∴∠APQ为直线PA与平面BPE所成角
在Rt△APQ中，AP=
，AQ=∴
，故答案为
点评：本题主要考查了直线与平面的所成角，以及解三角形等知识，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
相关题目
如图，半径为R的半球内有一内接正六棱锥P-ABCDEF，则直线PA与平面PBE所成的角大小为
如图，半径为R的半球内有一内接正六棱锥P-ABCDEF，则直线PA与平面BPE所成角正弦值是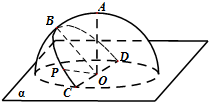
（2012•四川）如图，半径为R的半球O的底面圆O在平面α内，过点O作平面α的垂线交半球面于点A，过圆O的直径CD作平面α成45°角的平面与半球面相交，所得交线上到平面α的距离最大的点为B，该交线上的一点P满足∠BOP=60°，则A、P两点间的球面距离为（ ）
