题目内容
设实数a使得不等式|2x-a|+|3x-2a|≥a2对任意实数x恒成立,则满足条件的a所组成的集合是________.
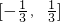
分析:根据所给的含有绝对值的不等式,设出所给的两个变量之间的关系,对所给的绝对值不等式进行整理,得到最简形式,根据函数的思想f(x)>m恒成立,只要m<f(x)的最小值.
解答:取k∈R,令
 ,则原不等式为|ka-a|+|
,则原不等式为|ka-a|+| ka-2a|≥|a|2,即|a||k-1|+
ka-2a|≥|a|2,即|a||k-1|+ |a||k-
|a||k- |≥|a|2
|≥|a|2由此易知原不等式等价于
 ,对任意的k∈R成立.
,对任意的k∈R成立.由于|k-1|+
 |k-
|k- |=
|=
∵y=
 ,在k
,在k 时,y
时,y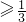
y=1-
 k,在1≤k<
k,在1≤k< 时,
时,
y=3-
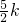 ,k<1时,y>
,k<1时,y>
所以|k-1|+
 |k-
|k- |的最小值等于
|的最小值等于 ,
,从而上述不等式等价于
 .
.故答案为:[-
 ]
]点评:本题考查函数的恒成立问题,考查含有绝对值的不等式的整理,考查函数的综合题目中常用的解题思想,f(x)>m恒成立,只要m<f(x)的最小值,本题解题的关键是求出函数的最小值,本题是一个难题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目