题目内容
11．当|$\overrightarrow{a}$$•\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$|，则$\overrightarrow{a}$，$\overrightarrow{b}$的位置关系是$\overrightarrow{a}$∥$\overrightarrow{b}$．分析 代入夹角公式计算向量的夹角，得出结论．
解答 解：∵|$\overrightarrow{a}$$•\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$|，∴$\overrightarrow{a}$$•\overrightarrow{b}$=±|$\overrightarrow{a}$||$\overrightarrow{b}$|，∴cos＜$\overrightarrow{a}，\overrightarrow{b}$＞=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=±1．
∴＜$\overrightarrow{a}，\overrightarrow{b}$＞=0或＜$\overrightarrow{a}，\overrightarrow{b}$＞=π．∴$\overrightarrow{a}$∥$\overrightarrow{b}$．
故答案为$\overrightarrow{a}$∥$\overrightarrow{b}$．
点评 本题考查了平面向量的夹角计算，向量的位置关系判断，属于基础题．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
6．三棱柱ABC-A1B1C1的所有棱长郡相等，∠A1AB=∠A1AC=120°，则AB1与BC1所成角的余弦值为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{2}$ | D． | 0 |
16．若向量$\overrightarrow{a}$、$\overrightarrow{b}$，满足|$\overrightarrow{a}$|=1、|$\overrightarrow{b}$|=$\sqrt{2}$，$\overrightarrow{a}$⊥（$\overrightarrow{a}+\overrightarrow{b}$），则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{2π}{3}$ | C． | $\frac{3π}{4}$ | D． | $\frac{5π}{6}$ |
20．设m，n是两条不同的直线，α，β是两个不同的平面，则下列结论正确的是（ ）
| A． | 若m∥α，n∥β且α⊥β，则m⊥n | B． | 若m∥α，n∥β且α⊥β，则m∥n | ||
| C． | 若m⊥α，n∥m且α∥β，则m⊥n | D． | 若m∥α，n∥β且α∥β，则m∥n |
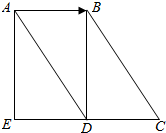如图所示，四边形ABCD是平行四边形，四边形ABDE是矩形．