题目内容
如图所示,ABCD为正方形,SA⊥平面ABCD,过点A作直于SC的平面分别交SB、SC、SD于点E、F、G,试判断AE与SB、AG与SD的位置关系,并说明理由.

答案:略
解析:
解析:
|
解: AE与SB,AG与SD的位置关系都是垂直.证明:∵ SC⊥平面AEFG,AG AEFG,AE AEFG,AE 平面AEFG, 平面AEFG,
∴ SC⊥AE,SC⊥AG.又∵ SA⊥平面ABCD,CD 平面ABCD,CB 平面ABCD,CB 平面ABCD, 平面ABCD,
∴ SA⊥CD,SA⊥CB.∵ ABCD是正方形,∴CD⊥AD,CB⊥AB.∵ AD∩SA=A,∴CD⊥平面SAD.又AG 平面SAD,∴CD⊥AG. 平面SAD,∴CD⊥AG.
∴ SC∩CD=C,∴AG⊥平面SDC.又SD 平面SDC.∴SD⊥AG. 平面SDC.∴SD⊥AG.
同理 AE⊥SB. |

练习册系列答案
相关题目
 如图所示,ABCD为正方形,SA⊥平面ABCD,过A且垂直于SC的平面分别交SB,SC,SD于E,F,G.求证:AE⊥SB,AG⊥SD.
如图所示,ABCD为正方形,SA⊥平面ABCD,过A且垂直于SC的平面分别交SB,SC,SD于E,F,G.求证:AE⊥SB,AG⊥SD.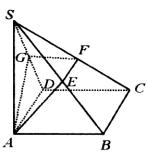

 如图所示,ABCD为梯形,
如图所示,ABCD为梯形,