题目内容
如图所示,四边形ABCD为正方形,?SA=SB=SC=SD,P是棱SC上的点,M、N分别是棱SB、SD上的点,SP∶PC=1∶2,SN∶ND=2∶1,SM∶MB=2∶1.求证:SA∥平面PMN.
证明:如图,取SC的中点E,连结AC交BD于O,连结OE.

∵在△CSA中,O为AC中点,E为SC中点,
∴OE∥SA.
设SO∩MN=F,连结PF.
又∵SN∶ND=2∶1,SM∶MB=2∶1,
∴在△SBD中,MN∥BD.
∴SF∶FO=SN∶ND=2∶1.
又∵SP∶PC=1∶2,E为SC中点,
∴SP∶PE=2∶1.∴SP∶PE=SF∶FO.
∴在△SOE中,PF∥OE.∴PF∥SA.
又SA?平面PMN,PF![]() 平面PMN,
平面PMN,
∴SA∥平面PMN.

练习册系列答案
相关题目



 (2012•许昌县一模)如图所示四边形ABCD内接于E、O,AC交BD于点E,圆的切线DF交BC的延长线于F,CD平分∠BDF
(2012•许昌县一模)如图所示四边形ABCD内接于E、O,AC交BD于点E,圆的切线DF交BC的延长线于F,CD平分∠BDF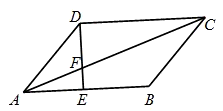
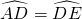 ,AB=10,BD=8,求cos∠BCE的值.
,AB=10,BD=8,求cos∠BCE的值.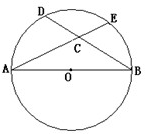
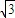 ,求切线DF的长.
,求切线DF的长.
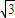 ,求切线DF的长.
,求切线DF的长.