题目内容
20．已知f（x）=x2-px+q，集合A={x|f（x）=x}={2}，求f（x）的表达式．分析 题目转化为x=2为方程x2-px+q=x的相等实根，由韦达定理可得．
解答 解：∵f（x）=x2-px+q，集合A={x|f（x）=x}={2}，
∴x=2为方程x2-px+q=x即x2-（p+1）x+q=0的相等实根，
∴由韦达定理可得$\left\{\begin{array}{l}{2+2=p+1}\\{2×2=q}\end{array}\right.$，解得$\left\{\begin{array}{l}{p=3}\\{q=4}\end{array}\right.$，
∴f（x）的表达式为f（x）=x2-3x+4
点评 本题考查函数解析式求解的待定系数法，属基础题．
练习册系列答案
相关题目
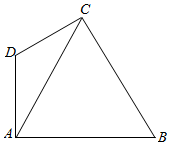滨湖区拟建一主题游戏园，该游戏园为四边形区域ABCD，其中三角形区城ABC为主题活动区，其中∠ACB=60°，∠ABC=45°，AB=12$\sqrt{6}$m；AD、CD为游客通道（不考虑宽度），且∠ADC=120°，通道AD、CD围成三角形区域ADC为游客休闲中心，供游客休憩．