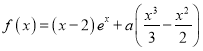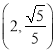题目内容
【题目】已知曲线![]() 的参数方程为
的参数方程为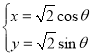 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为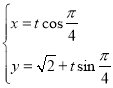 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线![]() 与曲线
与曲线![]() 的公共点的极坐标;
的公共点的极坐标;
(2)若点![]() 的极坐标为
的极坐标为![]() ,设曲线
,设曲线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,则在曲线
,则在曲线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的直角坐标,若不存在,请说明理由.
的直角坐标,若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)存在,点
;(2)存在,点
【解析】
(1)先求出曲线![]() 和
和![]() 的直角坐标方程,联立方程求得两曲线的公共点的直角坐标,再转化为极坐标;
的直角坐标方程,联立方程求得两曲线的公共点的直角坐标,再转化为极坐标;
(2)求出点![]() 和点
和点![]() 的直角坐标,假设存在点
的直角坐标,假设存在点![]() 满足条件,设点
满足条件,设点![]() ,求得
,求得![]() ,
,![]() ,由题意得
,由题意得![]() ,结合数量积的坐标表示即可求出答案.
,结合数量积的坐标表示即可求出答案.
解:(1)由题知,曲线![]() 消去参数
消去参数![]() 得到曲线
得到曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
曲线![]() 消去参数
消去参数![]() 得到曲线
得到曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
联立![]() 与
与![]() 的直角坐标方程
的直角坐标方程 解得
解得 或
或 ,
,
故两曲线的公共点的直角坐标为![]() 和
和![]() ,
,
∴曲线![]() 与曲线
与曲线![]() 的公共点的极坐标为
的公共点的极坐标为![]() ,
,![]() ;
;
(2)点![]() 的直角坐标为
的直角坐标为![]() ,点
,点![]() 的直角坐标为
的直角坐标为![]() ,
,
假设存在点![]() 满足条件,不妨设点
满足条件,不妨设点![]() ,
,
则![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,且
,且![]() ,
,
得![]() ,
,
化简得![]() ,又
,又![]() ,
,
得![]() ,
,![]() ,
,
所以点 ,
,
即在曲线![]() 上存在点
上存在点 ,使得
,使得![]() .
.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】交强险是车主必须为机动车购买的险种,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系.每年交强险最终保险费计算方法是:交强险最终保险费![]() ,其中a为交强险基础保险费,A为与道路交通事故相联系的浮动比率,同时满足多个浮动因素的,按照向上浮动或者向下浮动比率的高者计算.按照我国《机动车交通事故责任强制保险基础费率表》的规定:普通6座以下私家车的交强险基础保险费
,其中a为交强险基础保险费,A为与道路交通事故相联系的浮动比率,同时满足多个浮动因素的,按照向上浮动或者向下浮动比率的高者计算.按照我国《机动车交通事故责任强制保险基础费率表》的规定:普通6座以下私家车的交强险基础保险费![]() 为950元,交强险费率浮动因素及比率如下表:
为950元,交强险费率浮动因素及比率如下表:
交强险浮动因素和浮动费率比率表 | ||
类型 | 浮动因素 | 浮动比率 |
| 上一个年度未发生有责任道路交通事故 |
|
| 上两个年度未发生有责任道路交通事故 |
|
| 上三个及以上年度未发生有责任道路交通事故 |
|
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及以上有责任道路交通事故 |
|
| 上一个年度发生有责任道路交通死亡事故 |
|
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了100辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计结果如下表:
类型 |
|
|
|
|
|
|
数量 | 25 | 10 | 10 | 25 | 20 | 10 |
以这100辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题.
(1)记X为一辆该品牌车在第四年续保时的费用,求X的分布列与数学期望(数学期望值保留到个位数字);
(2)某二手车销售商专门销售这一品牌的二手车,且将经销商购车后下一年的交强险最终保险费高于交强险基础保险费![]() 的车辆记为事故车,假设购进一辆事故车亏损3000元,购进一辆非事故车盈利5000元.
的车辆记为事故车,假设购进一辆事故车亏损3000元,购进一辆非事故车盈利5000元.
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至少有一辆是事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望.
【题目】区块链技术被认为是继蒸汽机、电力、互联网之后,下一代颠覆性的核心技术区块链作为构造信任的机器,将可能彻底改变整个人类社会价值传递的方式,2015年至2019年五年期间,中国的区块链企业数量逐年增长,居世界前列现收集我国近5年区块链企业总数量相关数据,如表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号 | 1 | 2 | 3 | 4 | 5 |
企业总数量y(单位:千个) | 2.156 | 3.727 | 8.305 | 24.279 | 36.224 |
注:参考数据![]() (其中z=lny).
(其中z=lny).
附:样本(xi,yi)(i=1,2,…,n)的最小二乘法估计公式为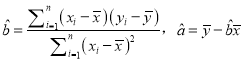
(1)根据表中数据判断,y=a+bx与y=cedx(其中e=2.71828…,为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由)
(2)根据(1)的结果,求y关于x的回归方程(结果精确到小数点后第三位);
(3)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三家区块链公司参赛比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,该公司就获得此次信息化比赛的“优胜公司”,已知在每场比赛中,甲胜乙的概率为![]() ,甲胜丙的概率为
,甲胜丙的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() ,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?