题目内容
在半径为2的圆内随机地取一点
，以点为中点做一条弦
，求弦长超过圆内接正三角形的边长概率是多少
A．
B．
C．
D．
【答案】
C
【解析】
试题分析：由题意可得：符合条件的点必须在内接等边三角形的内切圆内，理由如下：因为两圆的圆心相同，大圆的半径为1，故内接正三角形的边长为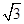
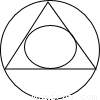
故内接等边三角形的内切圆半径为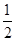
，故所求的概率为
，故选C
考点：本题考查了几何概型的求解
点评：此类几何概型问题，找到各自的度量是解决问题的关键，属中档题．
练习册系列答案
相关题目