题目内容
(本小题满分14分)设 、
、 是焦距为
是焦距为 的椭圆
的椭圆 的左、右顶点,曲线
的左、右顶点,曲线 上的动点
上的动点 满足
满足 ,其中,
,其中, 和
和 是分别直线
是分别直线 、
、 的斜率.
的斜率.
(1)求曲线 的方程;
的方程;
(2)直线 与椭圆
与椭圆 只有一个公共点且交曲线
只有一个公共点且交曲线 于
于 两点,若以线段
两点,若以线段 为直径的圆过点
为直径的圆过点 ,求直线
,求直线 的方程.
的方程.
(1) ;(2)3x+2y+5=0.
;(2)3x+2y+5=0.
【解析】
试题解析:(1)由已知椭圆中, ,∴
,∴ ,解得a=2,
,解得a=2,
所以 A,B的坐标为 A(1,0), B(1,0) . 2 分
设P(x, y),则由已知可得 ,即
,即 ,
,
所以曲线 的方程为
的方程为 . 5 分
. 5 分
(2)若直线MN 垂直x轴,则与曲线 只有一个交点,与题意不符,所以直线MN 存
只有一个交点,与题意不符,所以直线MN 存
在斜率,故设直线MN 的方程为:y=kx+m, 6 分
代入椭圆 方程
方程 整理,得
整理,得 ,
,
由题意可得直线与椭圆相切,故 ,
,
即 ① 7 分
① 7 分
将y=kx+m代入 ,整理得
,整理得 ,
,
设 ,则
,则 ②
②
且 , 8 分
, 8 分
故 ?
?
 ? 10 分
? 10 分
由以线段MN 为直径的圆过点B,所以BM⊥BN ,得m-k=-1 ③ 12分
由①③解得 ,经检验满足条件②
,经检验满足条件②
所以存在直线MN 满足条件,其方程为3x+2y+5=0. 14 分
考点:考查求曲线的方程,直线与圆,直线与抛物线的位置关系.

练习册系列答案
相关题目
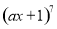 的展开式中,
的展开式中,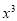 项的系数是
项的系数是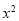 项系数和
项系数和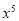 项系数的等比中项,则实数
项系数的等比中项,则实数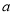 的值为
的值为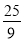 B.
B.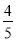 C.
C.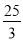 D.
D.
 ,向量
,向量 ,
, ,且
,且 ,则
,则 ___________.
___________. 为第二象限角,
为第二象限角, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 中,
中, 是圆
是圆

 ,垂足为
,垂足为 ,
,  ,垂足为
,垂足为 ,若
,若 ,
, ,则
,则 .
.
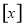 表示不超过
表示不超过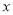 的最大整数,函数
的最大整数,函数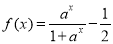
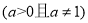 ,
,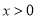 时恒有
时恒有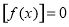 ,则实数
,则实数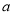 的取值范围是( )
的取值范围是( )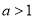 B.
B.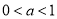 C.
C.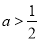 D.
D.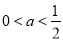
 ,
, ,
, ,
, ,
, 中任取两个不同字母,则取到字母
中任取两个不同字母,则取到字母 的概率为 .
的概率为 . 满足
满足 且
且 则向量
则向量 的夹角为__________.
的夹角为__________.