题目内容
如图,M、N、P分别是正方体ABCD—A1B1C1D1的棱AB、BC、DD1上的点.?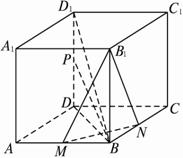
(1)若![]() ,求证:无论点P在D1D上如何移动,总有BP⊥MN;?
,求证:无论点P在D1D上如何移动,总有BP⊥MN;?
(2)若D1P∶PD=1∶2,且PB⊥平面B1MN,求二面角MB1NB的大小;?
(3)在棱DD1上是否存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.
(1)证明:若![]() ,则MN∥AC.?
,则MN∥AC.?
又∵正方体ABCD—A1B1C1D1,?
∴DD1⊥面ABCD.?
BD为BP在面ABCD上的投影.?
又∵BD⊥AC,AC![]() 面ABCD,?
面ABCD,?
∴BP⊥AC.又∵MN∥AC,∴BP⊥MN.?
(2)解析:设BP交平面B1MN于E,BD交MN于F,二面角M-B1N-B的大小为θ.?
∵MB⊥面BB1N,?
∴△BB1N为△MB1N在面BB1C1C上的投影,cosθ=![]() .?
.?
∵VB—MB1N?=![]() ×S△BB1N?×BM =
×S△BB1N?×BM =![]() ×S△B1MN?×BE,?
×S△B1MN?×BE,?
∴cosθ=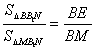 .?
.?
∵BP⊥面B1MN,∴BP⊥EF.?
又∵PD⊥BP,∴![]() .?
.?
∵BP⊥面B1MN,∴BP⊥MN.?
又∵BD为BP在面ABCD上的投影,则BD⊥MN,则BF=![]() BM.?
BM.?
又设正方体棱长为a,?
则PD=![]() a,BD=
a,BD=![]() a,BP=
a,BP=![]() a,?
a,?
![]() ,cosθ=
,cosθ=![]() ,tanθ=
,tanθ=![]() ,θ=arctan
,θ=arctan![]() .??
.??
(3)证明:若存在,过C作CQ⊥AC1于Q.再过Q作QQ1⊥面DCC1D1于Q1.在Rt△ACC1中,CQ⊥AC1,AC=![]() a,CC1=a,则C1Q∶QA=1∶2.?
a,CC1=a,则C1Q∶QA=1∶2.?
∴C1Q1∶Q1D=1∶2.?
∵面APC1⊥面ACC1,两面交于AC1,面ACC1中有CQ⊥AC1.
∴AC1⊥面APC1.∴AC1⊥PC1.?
又CQ1为CQ在面CDD1C1上的投影,且C1P ![]() 面CDD1C1,CQ⊥C1P,?
面CDD1C1,CQ⊥C1P,?
∴CQ1⊥C1P.设CQ1交C1D1于R.?
∴△CRC1≌△C1PD1.?
∴![]() .?
.?
又∵C1Q1∶Q1D=1∶2,
∴C1R∶CD=1∶2,R为C1D1的中点.?
∴P为DD1的中点.?
存在点P,P为DD1的中点.

 20、如图,在正方体ABCD-A1B1C1D1中,M、N、P分别为所在边的中点,O为面对角线A1C1的中点.
20、如图,在正方体ABCD-A1B1C1D1中,M、N、P分别为所在边的中点,O为面对角线A1C1的中点. 现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开.
现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开.

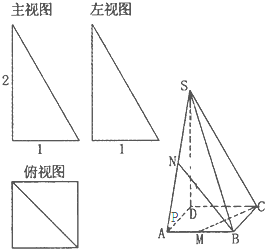 四棱锥S-ABCD的三视图和直观图如图所示,其中主视图和左视图为两个全等的直角三角形,俯视图为正方形,M,N,P分别为AB,SA,AD的中点.
四棱锥S-ABCD的三视图和直观图如图所示,其中主视图和左视图为两个全等的直角三角形,俯视图为正方形,M,N,P分别为AB,SA,AD的中点.