Question

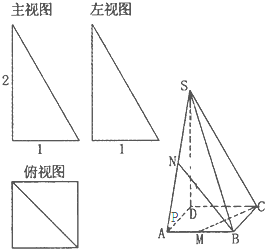四棱锥S-ABCD的三视图和直观图如图所示，其中主视图和左视图为两个全等的直角三角形，俯视图为正方形，M，N，P分别为AB，SA，AD的中点．
（1）求四棱锥S-ABCD的体积和表面积；
（2）求证：直线MC⊥平面BPN．

Answer 1

分析：（1）由三视图找到四棱锥的边长关系和垂直关系，进而求体积和表面积
（2）先证明线线垂直，再用线面垂直的判定定理证明线面垂直

解答：（1）解：由三视图知SD⊥底面ABCD，底面ABCD是正方形，AB=1，SD=2
∴底面ABCD的面积S=1×1=1
V_S-ABCD=

1

3

×S×SD=

1

3

×1×2=

2

3

又由题意知AB⊥AD，AB⊥SD，且AD∩SD=D
∴AB⊥面SAD
∴AD⊥SA
同理可证BC⊥SC
∴△SAB，△SBC是直角三角形
∴S_表=S_△SAD+S_△SCD+S_△SAB+S_△SBC+S=

1

2

×AD×SD+

1

2

×CD×SD+

1

2

×AB×SA+

1

2

×BC×SC+AB×BC
=

1

2

×1×2+

1

2

×1×2+

1

2

×1×

5

+

1

2

×1×

5

+1=3+

5

（2）证明：连接PN，PB，设PB∩CM=O
则PN∥SD
∴PN⊥面ABCD
又MC?面ABCD
∴PN⊥MC
∵在正方形ABCD中，P、M分别是AD、AB的中点
∴△PAB≌△MBC
∴∠PBA=∠MCB
又∠MCB+∠BMC=90°
∴∠PBA+∠BMC=90°
∴PB⊥MC
又PN∩PB=B，且PN、PB?面BPN
∴MC⊥面BPN

点评：本题考查由三视图求面积、体积，以及线面垂直的证明，要求能够从三视图中发现几何体的长度关系和平行垂直关系，能熟练应用线面垂直的判定定理．属简单题