Question

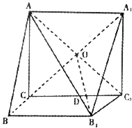（2007•淄博三模）如图所示，在直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，AB=2，BC=1，AA₁=

3

，D为棱CC₁的中点．
（I）证明：A₁C⊥平面AB₁C₁；
（Ⅱ）设平面AB₁C₁与平面ABD所成的角为θ，求cosθ；
（Ⅲ）在棱AB上是否存在一点E，使DE∥平面AB₁C₁？证明你的结论．

Answer 1

分析：（I）先证明BC⊥平面ACC₁A₁，可得B₁C₁⊥A₁C，再证明A₁C⊥AC₁，可得A₁C⊥平面AB₁C₁；
（II）建立空间直角坐标系，求出平面ABD的法向量，利用向量的夹角公式，即可得出结论；
（III）当点E为棱AB的中点时，DE∥平面AB₁C₁．证明平面EFD∥平面AB₁C₁即可．

解答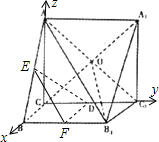：（I）证明：∵∠ACB=90°，∴BC⊥AC
∵三棱柱ABC-A₁B₁C₁为直三棱柱，∴BC⊥CC₁，
∵AC∩CC₁=C
∴BC⊥平面ACC₁A₁，
∵A₁C?平面ACC₁A₁，
∴BC⊥A₁C
∵BC∥B₁C₁，则B₁C₁⊥A₁C
∵Rt△ABC中，AB=2，BC=1，∴AC=

3

∵AA₁=

3

，四边形ACC₁A₁为正方形
∴A₁C⊥AC₁，
∵B₁C₁∩AC₁=C₁，
∴A₁C⊥平面AB₁C₁；
（Ⅱ）解：如图建立空间直角坐标系，则A（0，0，

3

），C（0，0，0），B（1，0，0），A1(0，

3

，

3

)，C1(0，

3

，0)，B1(1，

3

，0)，D(0，

3

2

，0)
由（ I）可知平面AB₁C₁的法向量为

CA1

=（0，

3， 3

）
设

n

=（x，y，z）为平面ABD的法向量．
∵

AB

=（1，0，-

3

），

AD

=(0，

3

2

，-

3

)
∴

x- 3 z=0 y-2z=0

令z=1，则x=

3

，y=2
∴

n

=（

3

，2，1）
∴cos＜

.

n

，

CA1

＞=

. n • CA1

| . n || CA1 |

=

3

4

∴cosθ=

3

4

；
（ III）解：当点E为棱AB的中点时，DE∥平面AB₁C₁．
证明如下：
如图，取BB₁的中点F，连EF，FD，DE
∵D，E，F分别为CC₁，AB，BB₁的中点；
∴EF∥AB₁，
∵AB₁?平面AB₁C₁，EF?平面AB₁C₁，
∴EF∥平面AB₁C₁，
同理可证FD∥平面AB₁C₁，
∵EF∩FD=F
∴平面EFD∥平面AB₁C₁，
∵DE?平面EFD
∴DE∥AB₁C₁．

点评：本题考查线面垂直，线面平行，线面角，考查学生分析解决问题的能力，考查向量知识的运用，属于中档题．