题目内容
12.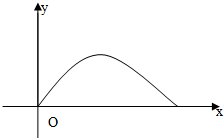 如图,在平面直角坐标系xOy中,x轴在地平面上,y轴垂直于地面,x轴、y轴上的单位长度都为1km,某炮位于坐标原点处,炮弹发射后,其路径为抛物线y=kx-$\frac{1}{20}(1+{k^2}){x^2}$的一部分,其中k与炮弹的发射角有关且k>0.
如图,在平面直角坐标系xOy中,x轴在地平面上,y轴垂直于地面,x轴、y轴上的单位长度都为1km,某炮位于坐标原点处,炮弹发射后,其路径为抛物线y=kx-$\frac{1}{20}(1+{k^2}){x^2}$的一部分,其中k与炮弹的发射角有关且k>0.(1)当k=1时,求炮弹的射程;
(2)对任意正数k,求炮弹能击中的飞行物的高度h的取值范围;
(3)设一飞行物(忽略大小)的高度为4km,试求它的横坐标a不超过多少km时,炮弹可以击中它.(答案精确到0.1,$\sqrt{5}$取2.236)
分析 (1)当k=1时,炮弹发射路径为$y=x-\frac{1}{10}{x^2}$,求出函数的零点,可得答案;
(2)根据二次函数的性质,求出最大高度的表达式,利用配方法可得h的取值范围;
(3)炮弹可以击中目标可化为:关于k的方程a2k2-20ak+a2+80=0有正解,由韦达定理,可得a的范围.
解答 解:(1)当k=1时,
炮弹发射路径为$y=x-\frac{1}{10}{x^2}$,
令y=0,解得x=0或10,
∴炮弹的射程为10km.…(4分)
(2)抛物线$y=kx-\frac{1}{20}(1+{k^2}){x^2}(k>0)$开口向下,
对称轴$x=-\frac{k}{{-\frac{1}{10}(1+{k^2})}}=\frac{10k}{{1+{k^2}}}$,
∴${y_{max}}=-\frac{1}{20}(1+{k^2}){(\frac{10k}{{1+{k^2}}})^2}+k(\frac{10k}{{1+{k^2}}})=\frac{{5{k^2}}}{{1+{k^2}}}=5-\frac{5}{{1+{k^2}}}<5$,
∴炮弹能击中的飞行物的高度h的范围是(0,5). …(9分)
(3)∵飞行物的高度为4km,它的横坐标a,
∴$4=ka-\frac{1}{20}(1+{k^2}){a^2}$,
整理得关于k的方程a2k2-20ak+a2+80=0有正解,…(11分)
显然a=0不满足方程a2k2-20ak+a2+80=0,
∴${k_1}+{k_2}=\frac{20}{a}$,${k_1}{k_2}=\frac{{{a^2}+80}}{a^2}>0$,
当a<0,k1,k2<0,不符题意,
∴a>0,k1,k2>0…(13分)
∴△=400a2-4a2(a2+80)≥0,解得$0<a≤2\sqrt{5}$,
∴飞行物的横坐标a不超过$2\sqrt{5}$km,约4.5km. …(16分)
(说明:过程不严密的适当扣分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

| A. | 4 | B. | 6 | C. | 7 | D. | 8 |
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
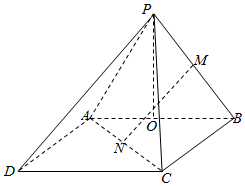 如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=$\frac{\sqrt{2}}{2}$,PC=$\sqrt{2}$且N为线段AC的中点,M为侧棱PB的中点,O为线段AB的中点,
如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=$\frac{\sqrt{2}}{2}$,PC=$\sqrt{2}$且N为线段AC的中点,M为侧棱PB的中点,O为线段AB的中点,