Question

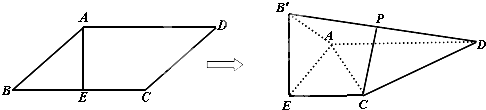
如图，已知平行四边形ABCD中，AD=2，CD=

2

，∠ADC=45°，AE⊥BC，垂足为E，沿直线AE将△BAE翻折成△B′AE，使得平面B′AE⊥平面AECD．连接B′D，P是B′D上的点．
（I）当B′P=PD时，求证CP⊥平面AB′D；
（Ⅱ）当B′P=2PD时，求二面角P-AC-D的余弦值．

Answer 1

分析：（1）利用面面垂直的性质，证出EC、EA、EB'两两互相垂直，因此建立空间直角坐标系如图所示．得出A、B'、C、D、E和P各点的坐标后，可得向量

AB‘

、

AD

、

CP

坐标，从而算出

CP

•

AB‘

=0，得到CP⊥AB'．同理CP⊥AD，结合线面垂直判定定理，即可证出CP⊥平面AB′D；
（2）根据

B′P

=2

PD

，算出P（

4

3

，

2

3

，

1

3

），利用垂直的两个向量数量积为0的方法，建立方程组解出

m

=（1，1，-3）为平面PAC的一个法向量，而平面DAC的一个法向量为

n

=（0，0，1），由空间向量的夹角公式，算出得cos＜

m

，

n

＞=

3 11

11

，即可得出二面角P-AC-D的余弦值．

解答：解：（1）∵AE⊥B'E，平面B′AE⊥平面AECD，平面B′AE∩平面AECD=AE
∴B'E⊥平面AECD，结合EC?平面AECD，可得B'E⊥CE
分别以EC、EA、EB'为x、y、z轴，建立空间直角坐标系如图所示．
可得A（0，1，0），B'（0，0，1），C（1，0，0），D（2，1，0），E（0，0，0），P（1，

1

2

，

1

2

）．

AB‘

=（0，-1，1），

AD

=（2，0，0），

CP

=（0，

1

2

，

1

2

）．
∵

CP

•

AB‘

=0×0+（-1）×

1

2

+1×

1

2

=0，
∴

CP

⊥

AB‘

，即CP⊥AB'．同理可得CP⊥AD
又∵AB'、AD是平面AB′D内的相交直线，
∴CP⊥平面AB′D；
（2）设P（x，y，z），可得

B′P

=（x，y，z-1），

PD

=（2-x，1-y，-z）
∵B'P=2PD，即

B′P

=2

PD

，可得x=

4

3

，y=

2

3

，z=

1

3

∴P（

4

3

，

2

3

，

1

3

），得

AP

=（

4

3

，-

1

3

，

1

3

），

AC

=（1，-1，0）
设平面PAC的法向量为

m

=（p，q，r），则

m • AP = 4p 3 - q 3 + r 3 =0 m • AC =p-q=0

．
取p=1，得q=1，r=-3，则

m

=（1，1，-3），
又∵平面DAC的一个法向量为

n

=（0，0，1），
∴由空间向量的夹角公式，得cos＜

m

，

n

＞=

m • n

|m| • |n|

=

3 11

11

．
由此可得二面角P-AC-D的余弦值等于

3 11

11

．

点评：本题在特殊的四棱锥中求证空间的垂直位置关系，并求二面角的大小．着重考查了空间直线和平面垂直的判定、二面角的定义及其求法等知识，属于中档题．同时考查了空间想象能力和推理论证能力．利用空间向量的方法降低思维难度，思路相对固定，是解决几何体问题的一种有效方法．