题目内容
如图,已知三棱锥P—ABC中,PA⊥平面ABC,AB=PA=a,且△ABC为正三角形,M、N为边PB、PC上的点,PC⊥平面AMN.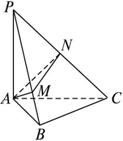
(1)求PB与平面PAC所成的角;
(2)求![]() 的值;
的值;
(3)求二面角P-AM-N的大小.
解:(1)取AC中点D,连结BD、PD.
∵PA⊥平面ABC,PA![]() 平面PAC,△ABC为正三角形,
平面PAC,△ABC为正三角形,
∴BD⊥平面PAC,PD为PB在平面PAC上的射影.
∴∠BPD即为PB与平面PAC所成的角.
由PA=AB=a得BD=![]() a,PB=
a,PB=![]() a,∴sin∠BPD=
a,∴sin∠BPD=![]() =
=![]() .
.
∴∠BPD=arcsin![]() ,即PB与平面PAC所成的角为arcsin
,即PB与平面PAC所成的角为arcsin![]() .
.
(2)由PC⊥平面AMN知PC⊥AN,MN⊥PC.
又△PAC为等腰直角三角形,PA=AC.
∴N为PC中点.PN=![]() a.
a.
在△BPC中,cos∠BPC=![]() =
=![]() .
.
在Rt△MPN中,PM=![]() =
=![]() a.
a.
∴MB=![]() a-
a-![]() a=
a=![]() a.∴
a.∴![]() =2.
=2.
(3)过N作NE⊥AM于E.连结PE.
∵PN⊥平面AMN,∴NE为PE在平面AMN上的射影.
∴PE⊥AM.∴∠PEN为二面角P-AM-N的平面角.
在△PAM中,∠APM=45°,AP=a,PM=![]() a.
a.
∴AM=a2+(![]() =
=![]() a.
a.
∴![]() AM·PE=
AM·PE=![]() PA·AM·sin∠APM.
PA·AM·sin∠APM.
∴PE= a·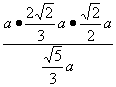 .
.
∴sin∠PEN=![]() =
=![]() =
=![]() .∴∠PEN=arcsin
.∴∠PEN=arcsin![]() ,
,
即二面角P-AM-N的大小为arcsin![]() .
.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 如图,已知三棱锥P-ABC中,PA⊥平面ABC,AN⊥BC于N,D是AB的中点,且PA=1,AN=BN=CN=
如图,已知三棱锥P-ABC中,PA⊥平面ABC,AN⊥BC于N,D是AB的中点,且PA=1,AN=BN=CN= 如图,已知三棱锥P-ABC中,PA⊥面ABC,其中正视图为Rt△PAC,AC=2
如图,已知三棱锥P-ABC中,PA⊥面ABC,其中正视图为Rt△PAC,AC=2 如图,已知三棱锥P-ABC的侧面PAB是等边三角形,D是AB的中点,PC=BC=AC=2,PB=2
如图,已知三棱锥P-ABC的侧面PAB是等边三角形,D是AB的中点,PC=BC=AC=2,PB=2 如图,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB的中点,且△PDB是正三角形,PA⊥PC.
如图,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB的中点,且△PDB是正三角形,PA⊥PC. (2009•河西区二模)如图,已知三棱锥P-ABC中,底面△ABC是边长为
(2009•河西区二模)如图,已知三棱锥P-ABC中,底面△ABC是边长为