题目内容
4．若复数z1满足（z1-z）（1+i）=1-i（i为虚数单位），复数z2的虚部为2，z1•z2是实数．（1）求z2
（2）若|z|=1，求|z-z2|的最小值．
分析 （1）由（z1-2）（1+i）=1-i，解得z1=2-i，设z2=a+2i，a∈R，则z1z2=（2-i）（a+2i）=（2a+2）+（4-a）i，由z1•z2∈R，能求出z2；
（2）利用复数模的几何意义数形结合得答案．
解答 解：（1）∵（z1-2）（1+i）=1-i，
∴z1-2=$\frac{1-i}{1+i}=\frac{（1-i）^{2}}{（1+i）（1-i）}=\frac{-2i}{2}=-i$，
∴z1=2-i，
设z2=a+2i，a∈R，
则z1z2=（2-i）（a+2i）=（2a+2）+（4-a）i，
∵z1•z2∈R，
∴a=4，
∴z2=4+2i；
（2）∵|z|=1，如图，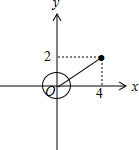
∴|z-z2|的最小值为$\sqrt{{4}^{2}+{2}^{2}}-1=2\sqrt{5}-1$．
点评 本题考查复数的代数形式的混合运算，考查了复数模的求法，体现了数形结合的解题思想方法，是基础题．
练习册系列答案
相关题目
．记∠ACD＝
，∠BCD＝
．
；
，求BC 的长．