题目内容
已知等比数列 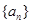 的所有项均为正数,首项
的所有项均为正数,首项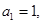 且
且 成等差数列.
成等差数列.
(1)求数列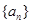 的通项公式;
的通项公式;
(2)数列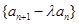 的前
的前 项和为
项和为 若
若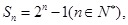 求实数
求实数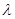 的值.
的值.
【答案】
(1) =
=
 ;(2)
;(2) .
.
【解析】
试题分析:(1)利用 为等差中项列式求解;(2)记
为等差中项列式求解;(2)记 ,证明其为等比数列,求出前
,证明其为等比数列,求出前 项和,用已知的
项和,用已知的 待定系数可得
待定系数可得 .
.
试题解析:(1)设数列 的公比为
的公比为 ,由条件得
,由条件得 成等差数列,
成等差数列,
所以 2分
2分
解得
由数列 的所有项均为正数,则
的所有项均为正数,则 =2 4分
=2 4分
数列 的通项公式为
的通项公式为 =
=
 6分
6分
(2)记 ,则
,则 7分
7分
若 不符合条件; 8分
不符合条件; 8分
若 ,
则
,
则 ,数列
,数列 为等比数列,首项为
为等比数列,首项为 ,公比为2,
,公比为2,
此时 11分
11分
又 =
= ,所以
,所以 13分
13分
考点:1.等比数列;2.等差数列;3.数列求和.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 的所有项均为正数,首项
的所有项均为正数,首项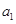 =1,且
=1,且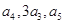 成等差数列.
成等差数列.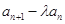 }的前
}的前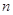 项和为
项和为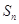 ,若
,若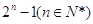 ,求实数
,求实数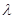 的值.
的值. 的首项
的首项 ,公比
,公比 ,数列
,数列 项的积记为
项的积记为 .
. ,证明:数列
,证明:数列 为等比数列.
为等比数列. )
)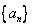 的首项为
的首项为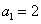 ,公比为
,公比为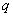 (
(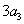 是
是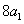 与
与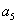 的等差中项;数列
的等差中项;数列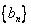 满足
满足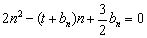 (
(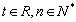 ).
).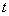 的值,使得数列
的值,使得数列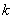 ,在
,在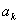 与
与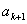 之间插入2共
之间插入2共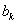 个,得到一个新数列
个,得到一个新数列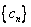 .设
.设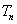 是数列
是数列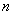 项和,试求满足
项和,试求满足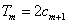 的所有正整数
的所有正整数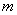 的值。
的值。