题目内容
在直角坐标系中,已知点P(x,y).O为坐标原点.
(1)若
(其中a、b、r是常数,且r>0),求证:(x-a)2+(y-b)2=r2.
(2)若点A(2,4),M(2x-1,22y-1),N(4y,2x),
•
=-1,求u=
•
的取值范围.
(1)若
|
(2)若点A(2,4),M(2x-1,22y-1),N(4y,2x),
| OP |
| AP |
| ON |
| OM |
(1)由cos2θ+cos2θ=1 消去θ即得 (x-a)2+(y-b)2=r2.
(2)由
•
=-1,可得 x(x-2)+y(y-4)=-1,∴(x-1)2+(y-2)2=4.
令x=1+2cosθ,y=2+2sinθ,又u=
•
=2x-1•4y +22y-1•2x =2x+2y ,
又x+2y=5+2cosθ+4sinθ=5+2
sin(θ+∅),cos∅=
,sin∅=
,
∴5-2
≤x+2y≤5+2
,∴u的取值范围为[25-2
,25+2
].
(2)由
| OP |
| AP |
令x=1+2cosθ,y=2+2sinθ,又u=
| ON |
| OM |
又x+2y=5+2cosθ+4sinθ=5+2
| 5 |
| 2 | ||
|
| 1 | ||
|
∴5-2
| 5 |
| 5 |
| 5 |
| 5 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
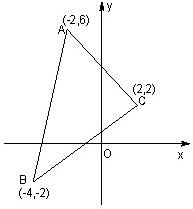 如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求:
如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求: 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: